Из уравнения Максвелла мы имеем волновые уравнения для ![]() и
и ![]()
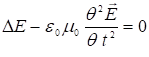 и
и 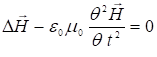 (1)
(1)
в вакууме. Сравнивая с волновым уравнением для любой физической величины
![]() ,
, 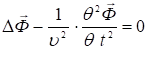 (2)
(2)
имеем
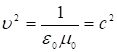 , (3)
, (3)
где с – const=3×108 м/c.
Для скорости в среде 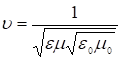 ; или
; или 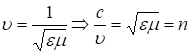 – показатель преломления среды.
– показатель преломления среды.
Уравнение (2) для одномерного случая имеет решения
Ф(x,t)=Ф1(x+ct)+Ф2(x-ct) (4)
В виде суперпозиции двух волн.
В случае гармонических волн имеем, например, для
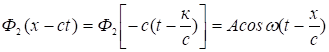 . (5)
. (5)
Это плоская гармоническая волна.
Для положительного направления в общем случае имеем:
Ф(х,t)=Аcosω(t-x/c)+Bsinw(t-x/c), (6)
а для отрицательного направления :
Ф(х,t)=Аcosw(t+x/c)+Bsinw(t+x/c). (7)
Для представления волн в общекоординатной форме вводится волновой вектор ![]() , равный по модулю волновому числу
, равный по модулю волновому числу ![]() и направленный в положительном направлении.
и направленный в положительном направлении.
Для произвольной точки
![]() (8)
(8)
Это плоская волна, распространяющаяся в направлении вектора ![]() . Аналогично и для синуса
. Аналогично и для синуса
![]() . (9)
. (9)
Используя формулу Эйлера, получим:
![]() и
и ![]() (10)
(10)
Удобно пользоваться комплексным выражением для плоской волны в виде
![]() . (11)
. (11)
Здесь А может быть как действительной, так и комплексной или мнимой величиной.
Сферическая волна записывается в комплексной форме в виде:
![]() (12)
(12)
Здесь в показателе экспоненты стоит не скалярное произведение ![]() , а произведение положительных величин к
и r.
, а произведение положительных величин к
и r.
Фотометрия
Для исследования оптических явлений вводятся различные величины как объективные (энергетические), так и субъективные (фотометрические). Дело в том, что и приборы и человеческий орган зрения – глаз не регистрируют полностью энергию переносимую электромагнитными волнами, а воспринимают избирательно. Например, глаз наиболее чувствителен к длине волны 555 нм.
Поможем написать любую работу на аналогичную тему

