 В настоящее время широкое практическое применение находит многолучевая интерференция. В этом случае складываются волны, возникающие в результате многократного отражения и преломления между двумя полузеркальными поверхностями.
В настоящее время широкое практическое применение находит многолучевая интерференция. В этом случае складываются волны, возникающие в результате многократного отражения и преломления между двумя полузеркальными поверхностями.
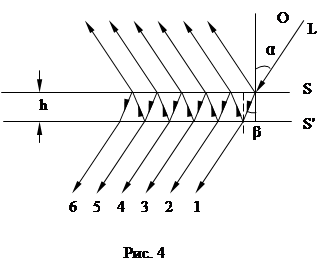
Пусть луч L падает на плоскопараллельную пластинку толщиной h с n>1, имеющую поверхности S и S¢ с коэффициентом отражения r и коэффициентом пропускания g (рис. 4). Коэффициент пропускания пластинки t, показатель преломления n>1. Проведем сложение волн в прошедшем свете. Падающую волну запишем в виде
E=E0eiωt (6)
тогда E1=E0γ2τeiФ', где ![]() , Δ=2nhcosβ.
, Δ=2nhcosβ.
E2=(E0γ2τeiФ')τ2ρ2e-iФ, где ![]() .
.
Здесь d1 и d2 скачки фазы при отражении. E3=(E0γ2τeiФ')τ4ρ4e-2iФ и т.д.
EN=(E0γ2τeiФ')τ2(N-2)ρ2(N-1)e-i(N-1)Ф.
Этот ряд представляет геометрическую прогрессию с первым членом Е1 и знаменателем τ2ρ2e-iФ .
Сумма ее
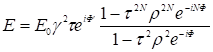 (7)
(7)
при a®0, N®¥.
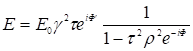 (8)
(8)
Перейдем к интенсивности, для чего это значение Е умножим на сопряженную Е*
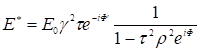 (9)
(9)
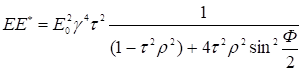 (10)
(10)
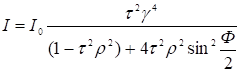 (11)
(11)
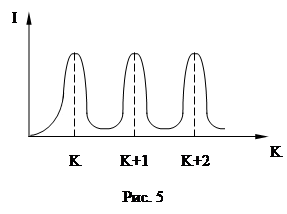 График интенсивности прошедшего света имеет вид рис. 5. Рассмотрим условие максимумов. I максимальна при
График интенсивности прошедшего света имеет вид рис. 5. Рассмотрим условие максимумов. I максимальна при ![]() (12)
(12)
учитывая, что Δ=2nhcosβ, имеем ![]() , при
, при ![]() имеем
имеем
2nhcosβ=кλ (13)
Поможем написать любую работу на аналогичную тему

