Когерентностью называется согласованное протекание нескольких колебательных или волновых процессов.
Рассмотрим две световые волны одинаковой частоты, которые создают в некоторой точке пространства колебания одинакового направления.
E1= E01sin(ωt+Ф1) и E2= E02sin(ωt+ Ф2) (1)
Амплитуда результирующего колебания будет
E0Р2 =E012+E022+2E01E02cos(Ф1-Ф2) (2)
Если разность фаз δ(t)= Ф1-Ф2 остается постоянной во времени, то волны будут когерентными. В случае некогерентных волн cosδ(t) принимает значения от -1 до 1 и среднее значение его будет равно 0, тогда
E0Р2= E012+E022 (3)
Средний по времени световой поток через единицу площади, установленной перпендикулярно направлению распространения волн называется интенсивностью света I. Световой поток определяется энергетическим, который задается вектором 
, а амплитуда вектора 
пропорциональна амплитуде вектора 
, следовательно 
~E2
и I~ E2.
Таким образом, интенсивность света при сложении двух волн будет
. (4)
Если складываются когерентные волны, то в точках, где cosδ(t)>0, I будет превышать I1+I2, а в точках, где cosδ(t)<0, I, будет меньше суммы I1+I2. Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве. В одних местах возникают максимумы, для которых
I=4I1 (если I1=I2 ) (5)
в других местах минимумы, где
I=0 (6).
Для некогерентных волн всюду одинаковая освещенность, так как везде
I=2I1 (7).
Явление перераспределения интенсивности света в пространстве при наложении когерентных световых волн называется интерференцией.
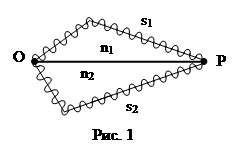Когерентные световые волны можно получать, если разделить с помощью отражения или преломления волну, испускаемую источником на две части (рис. 1). В точке О происходит разделение волны. Первая волна проходит до точки Р, где встречаются волны, в среде с показателем преломления n1, а вторая волна в среде с показателем n2. Геометрическая длина пути первой s1, а второй s2. В т. О фаза колебания wt, а в точке Р имеем
и 
, (8)
где υ1=с/n1 и υ2- с/n2 – фазовые скорости волн в соответствующих средах. Разность фаз δ(t) будет
(9)
Заменив ω/c через 2πν/c=2π/λ0 (l0 – длина волны в вакууме), получим
, (10)
где Δ = n2s2 – n1s1= L2 – L2 – оптическая разность хода, (11)
а L1 и L2 – оптическая длина пути.
Если Δ=±кλ0(к=0, 1, 2,…), (12)
то разность фаз будет кратной 2p и колебания в точке Р будут проходить в одинаковой фазе. Следовательно, это есть условие интерференционного максимума.
Если Δ равна полуцелому числу длин волн в вакууме
Δ=±(к+
)λ0
(к=0, 1, 2,…), (13)
то δ=±(к2π +π), т.е. в точке Р колебания находятся в противофазе. Это условие интерференционного минимума.
Для наблюдения интерференции в оптике существуют два метода: метод деления волнового фронта и метод деления амплитуды. Метод деления фронта волны используется только для источников достаточно малых размеров. В нем пучок света делится на два, либо проходя через два близко расположенных отверстия, либо отражаясь от зеркальных поверхностей (зеркала Френеля) и т.д. В методе делен амплитуды, который пригоден для протяженных источников, пучок света делится путем прохождения и отражения от полупрозрачной поверхности.
Когерентность лучей, исходящих от пространственно разделенных участков протяженного источника называется пространственной.
Рассмотрим условия, при которых возможно получить при этом интерференционную картину (рис. 2). Разность хода лучей Δ от крайних точек лучей А и В расходящихся под углом 2j
AN=BM=Δ=2bsinj, (14)
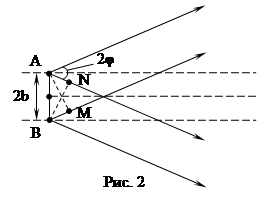где 2b расстояние между точками Аи В, 2j – угол раскрытия пучка. Равенство разности хода Δ четверти длины волны соответствует смещению интерференционной картины, полученной от точек А и В на полполосы. Интерференционная картина остается четкой, если такое смещение не превышает полполосы, т.е.
2bsinj≤λ/4 (15)
– условие пространственной когерентности, а угол 2j – апертура интерференции.
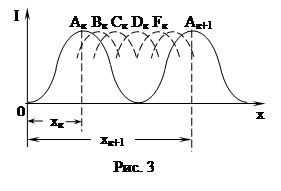
Если имеем немонохроматический свет, то на экране (рис. 3) получится интерференционная картина для всех длин волн спектра l, Δl.
Выясним условие различимости интерференционной картины. Задача заключается в нахождении Δl, при которой можно различить интерференционную картину.
Расстояние соответствующего максимума Aк, Bк, Cк, Oк, Fк для каждой длины волны от центра О прямо пропорционально длине волны. Интерференционная картина будет различимой, если расстояние между максимумами Ак и Ак+1 не будет заполнен максимумами остальных волн интервала Δl. Таким образом, критерием неразличимости интерференционной картины будет совмещение (к+1)-го порядка максимума волны l с к-м максимумом волны l +Δl, т.е.
x к+1(x)= x к(λ+Δλ) или (к+1)λ= к(λ+Δλ) (16)
Отсюда Δλпред=λ/к. Таким образом, для наблюдения интерференции немонохроматического света необходимо, чтобы ширина интервала длин волн не превышала предельного значения
Δλ< Δλпред= λ/к (17)
Вообще, для различимости интерференционной картины вводится величина, называемая видностью V, которая находится как
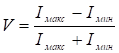(18)
В общем случае источники света испускают лучи различных волн, следующих друг за другом через беспорядочно меняющиеся промежутки времени. Прибор регистрирует картину, усредненную по времени. Если за время tприб., необходимое для срабатывания прибора, множитель cosδ(t) принимает все значения от -1 до +1, то среднее время интерференционного члена 
будет равно нулю и прибор не будет наблюдать интерференционную картину. Для наблюдения интерференции необходимо чтобы tприбора << tког
(время когерентности). За время когерентности принимается время, за которое случайное изменение фазы волны δ(t) достигает значения порядка π. Под длиной когерентности принимается длина
Lког=сtког (19)
Поможем написать любую работу на аналогичную тему