Если на пути распространения света поставить непрозрачный экран с отверстием, то в зависимости от размера отверстия получаются различные картины. Если диаметр отверстия велик, то на экране, где наблюдаем прошедший свет, получается такого же вида пучок. Если отверстие очень мало, то свет начинает заходить в область тени. Это явление отклонение света от прямолинейности распространения при встрече преграды называется дифракцией света.
Дифракция света объясняется принципом Гюйгенса-Френеля. Голландский физик Гюйгенс предложил считать, что свет представляет собой волны, которые распространяются в особой среде – эфире подобно звуку. Этот эфир заполняет все пространство и вещество. С этой точки зрения колебательное движение частиц эфира передается не только той частице, которая лежит на пути светового луча, но и всем частицам, примыкающим к этой частице, т.е. световая волна распространяется из данной точки во все стороны. Таким образом, каждая точка волнового фронта является источником вторичных волн. Френель добавил это тем, что эти источники являются когерентными, а испускаемые ими вторичные волны интерферируют.
Для нахождения интенсивности, источник ограничивается воображаемой замкнутой поверхностью любой формы. Эта поверхность рассматривается как светящаяся, и излучение отдельных элементов происходит в виде сферических волн, которые как когерентные накладываются в точке наблюдения.
Рассмотрим это на примере. Пусть точечный источник S (рис. 1) испускает сферическую волну, которая в момент времени t запишется в виде
(1)
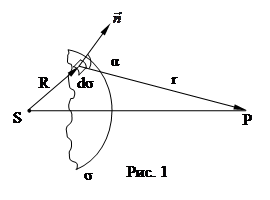Здесь R – радиус фронта, который представляет собой среду s выберем элемент этой поверхности ds, который принимается за точечный вторичный источник. В точке наблюдения Р этот элемент создает колебания так же в виде сферической волны радиусом r. Оно запишется в виде
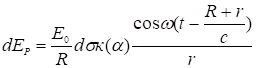(2)
– амплитудное значение. Здесь к(a) – коэффициент, учитывающий положение элемента ds относительно точки наблюдения. Определяется углом a между нормалью к элементу 
и направлением луча на точку наблюдения.
Для определения результирующего светового эффекта необходимо проинтегрировать по σ, т.е.
(3)
Поможем написать любую работу на аналогичную тему