ТОНКАЯ ЛИНЗА

Простейшей центрированной оптической системой является линза. Она представляет собой прозрачное (обычно стеклянное) тело, ограниченное двумя сферическими поверхностями (в частном случае одна из поверхностей может быть плоской). Точки пересечения поверхностей с оптической осью линзы называются вершинами преломляющих поверхностей. Расстояние между вершинами именуется  толщиной линзы. Если толщиной линзы можно пренебречь по сравнению с меньшим из радиусов кривизны ограничивающих линзу поверхностей, линза называется тонкой.

В случае тонкой линзы главные плоскости  и  можно считать совпадающими и проходящими через центр линзы  (рис. 3.1.12).  Для фокусных расстояний тонкой линзы получается выражение

;

здесь  - показатель преломления линзы,  - показатель преломления среды, окружающей линзу,  и  - радиусы кривизны поверхности линзы. С радиусами кривизны нужно обращаться, как  с алгебраическими величинами: для выпуклой поверхности (т. е. в случае, когда центр кривизны лежит справа от вершины) радиус кривизны нужно считать положительным, для вогнутой поверхности (т. е. в случае, когда центр кривизны лежит слева от вершины) радиус нужно считать отрицательным. На чертежах указываются модуль радиуса кривизны, т. е. , если .

Если показатели преломления сред, находящихся по обе стороны тонкой линзы, одинаковы, то узлы  и  совпадают с главными точками, т. е. помещаются в центре линзы . Следовательно, в этом случае любой луч, идущий через центр линзы, не изменяет своего направления. Если показатели преломления сред перед и за линзой неодинаковы, узлы не совпадают с главными точками, так что луч, идущий через центр линзы, претерпевает излом.

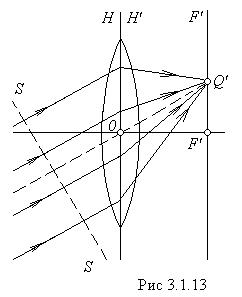
Параллельный пучок лучей после прохождения через линзу собирается в одной из точек фокальной плоскости (точка  на рис. 13). Чтобы определить положение этой точки, нужно продолжить идущий через центр  линзы луч до пересечения его с фокальной плоскостью (изображенный пунктиром луч ). В точке пересечения соберутся и остальные лучи. Такой способ пригоден в том случае, если оптические свойства среды по обе стороны линзы одинаковы (). В противном случае луч, идущий через центр, терпит излом. Для нахождения точки  в этом случае нужно знать положение узловых точек линзы.             

Отметим, что отложенные вдоль лучей пути, начинающиеся на волновой поверхности  ( рис. 3.1. 13) и заканчивающиеся в точке , имеют одинаковую оптическую длину и являются таутохронными.