ИНТЕРФЕРЕНЦИЯ.

Еще до создания электромагнитной теории света при  изучении  явления  ин-

терференции была  доказана поперечность  световых  волн. В  интерференции  на-

иболее отчетливо обнаруживают себя волновые  свойства  света. Это  явление  ха-

рактерно для волн любой природы и сравнительно просто  наблюдается  для  волн

на поверхности воды или для звуковых волн. Наблюдать  же интерференцию  све- товых волн можно лишь при определенных условиях.

Пусть с помощью некоторых оптических приспособлений происходит  нало-

жение одного светового пучка на другой. Если среда линейна, т.е.  ее  свойства  не

изменяются под действием возмущений, создаваемых световой волной,  то  к  ним

применим  принцип  суперпозиции.  Вследствие  закона  независимости  действия

световых пучков (принципа суперпозиции) при распространении в линейной  сре-

де каждый пучок будет проходить область так, как если  бы  другого  пучка  не су- ществовало.

(В нелинейной оптике принцип суперпозиции не выполняется. При  высокой

интенсивности, например, лазерных пучков, свет  меняет свойства  среды  и  через ее воздействует сам на себя - самовоздействие. В этом случае и  n  и  другие  вели- чины зависят от среды.)

Пусть -  напряженность  электрической  компаненты  поля,  создаваемого

первым пучком в произвольной точке области перекрытия, - вторым.

       Результирующая напряженность поля в той же точке:

Переходим к энергетическому описанию (интенсивность квадрата  амплиту-        ды):

Из-за очень  большой  частоты колебаний  для  оптической  области  спектра ω ~ (1015 с-1)  мгновенное значение напряженности  невозможно измерить непо-средственно. Всем приемникам присуща  определенная инерционность. Приемни- ки могут измерять  только  величины, квадратичные по полю, усредненые за вре- мена не меньшие времени разрешения приемника, т.е. за очень большое число периодов колебаний.Такими являются энергетические и фотометрические вели- чины: лучистый  и  световой  поток,  яркость,  освещенность, интенсивность. Ча- ще всего пользуются понятием интенсивности  светового пучка I, под которой будем понимать усредненное  по  времени  значение  вектора плотности потока энергии, т.е. среднее значение вектора Умова-Пойтинга.

Если напряженность электрического и магнитного полей изменяются по гар-

моническому закону  и  , то                                                          

                                        I =.

C учетом , получим окончательно

                               I =.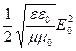

В явлении интерференции  представляет  интерес  относительное  изменение

этой величины, например,относительное распределение интенсивности на экране,

куда  попадает  свет.  Множитель 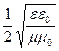  будет  постоянным  в  данной  среде  и

можно  считать,   что  интенсивность  равна  квадрату  амплитуды  напряженности

электрического поля  I = .

Электромагнитое поле волны определяется обоими векторами  и  .  Од-

нако именно вектор является световым и определяет действие света  на  органы

зрения, фотопластинки, фотоэлементы и  другие  приборы. С  точки  зрения  элек-

тронной теории действие света на электроны вещества  в  основном  определяется

электрическим   вектором  .  Указанные  утверждения   подтвержены   опытами

О.Винера, П.Друде, В.Нериста.

                                                     <

Слагаемое , учитывающее  взаимодействие  пучков,  называется

интерференционным членом.

Не будем рассматривать случай  наложения двух  плоских  монохроматичес-

ких волн разных частот,  когда . Рассмотрим  идеализированный  слу- чай, когда обе волны строго монохроматические и имеют одну частоту ω.

Монохроматическая волна – это строго гармоническая волна с постоянными

во времени частотой ω, амплитудой a и начальной фазой φ. Амплитуда и фаза  ко-

лебаний могут меняться от одной точки пространства к другой, частота одна  и  та

же для колебательного процесса во всем  пространстве. Монохроматическое коле-

бание в каждой точке пространства длится бесконечно долго, не  имея  ни  начала,

ни конца во времени. Поэтому строго монохроматические  колебания  никогда  не  могут быть точно реализованы в действительности реальными источниками. Тем не менее монохроматическая идеализация оказывается достаточной  для  решения  многих  задач.

В точке пространства, где  пересекаются эти два  монохроматических  свето- вых пучка:

будем иметь результируещее колебание:

                             .

При этом учитывая, что , можно записать:

                 I = I1 + I2 + 4, где I = , I1 = , I2 = - интенсив-

ности соответствующих полей.

В случае  равенства  интерференционного члена  нулю  результирующая  ин-                  тенсивность равна сумме интенсивностей накладываемых  пучков, и  интерферен-

ция отсутствует.

Под интерференцией понимают явление, при котором в результате  суперпо-

зиции световых волн происходит перераспределение  потока  световой  энергии  в 

пространстве, обусловленное суперпозицией ЭМВ, в результате чего в одних мес-

тах возникают усиления, а в других – ослабления интенсивности.

Очень   важный  случай  интерференции  наблюдается  при  наложении  двух

встречных плоских волн с одинаковой амплитудой, в результате  которого  возни-

кает стоячая волна.

         Таким  образом   неравенство   служит  необходимым   условием  возникновения  интерференции. Соответствующие  световые  пучки,  дающие  ин-

терференцию, являются коррелированными или когерентными  между собой. Ко- лебательные  и  волновые процессы в них протекают во времени согласованно. Говарят также, что когерентные пучки интерферируют, а некогерентные не интер- ферируют между собой.

Все сказанное о двух пучках относится  и  к  случаю  наложения  нескольких

пучков.Интерференция  двух пучков  называется  двух лучевой,  многих  пучков –

многолучевой.

Если взять независимые световые пучки, то, как  показывает  опыт  (впервые Дж.В.Стрэтт, Рэлей), результирующая интенсивность равна сумме интенсивно- стей  налагающихся пучков (например,естественные источники света: электричес-

 кие  лампы накаливания). Даже применение одинаковых светофильтров для мо- ‘нохроматизации’ излучения ламп  также  не  приводит  к  появлению интерфе- ренции. Этот результат является следствием того, что ни один реальный источник не дает  строго монохроматическгого света.

Немонохроматичность, а следовательно и некогерентность естественных ис-

точников света, обусловлена самим механизмом процесса  испускания  света  ато- мами (молекулами, ионами) светящегося  тела. Отдельные  атомы  излучают  цуги волн длительностью порядка 10-8с. За  это  время  возбужденный  атом   возвраща-  ется  в нормальное состояние и излучение им света  прекращается. Возбудившись  вновь, атом снова начинает испускать световые волны. Такое преривистое излу- чение света  атомами  в  виде  цугов  волн (отдельных  кратковременных импуль-  сов) характерно для любого источника света независимо от специфических осо- бенностей тех  процессов, которые происходят в источнике и вызывают возбуж- дение его атомов.

Каждый цуг  волн  имеет  ограниченную  протяженность  (около  3м). Вслед-

ствие этого он отличен  от  монохроматической  волны,  которая  по  определению

имеет неизменную амплитуду и неограничена в пространстве. Однако немонохро-

матичностью отдельного цуга волн можно пренебречь.

Атомы светящегося тела излучают свет  независимо  друг  от  друга. Началь-

ные фазы соответствующих им цугов волн никак не связаны  между  собой.  Даже

для одного и того же атома значения начальных фаз разных цугов  хаотически  из-

меняется от одного акта излучения этого атома  к  другому,  т.е.  фаза  результиру-

ющей волны претерпевает случайные изменения.

Таким образом свет,  испускаемый  монохроматическим  источником,  также

некогерентен.

Все сказанное выше справедливо только для спонтанного излучения  атомов

или молекул, осуществляющегося независимо от действия  какого-либо  внешнего

ЭМ поля. Индуцированное или вынужденное  излучение  системы  возбужденных

атомов или молекул, возникающее под действием переменного внешнего электро-

магнитного поля, когерентно с возбуждающим его монохроматическим излучени-

ем. Оно обладает  той же частотой, направлением распространения и  поляризаци-

ей. Пример: лазеры.

Рассмотрим более подробно интерференционный член

Отсюда следует, что если колебания в световых лучах перпендикулярны, т.е.

, то интерференционный  член  равен нулю  при  любых  фазовых  соотно-                шениях. Если же колебания в пучках не перпендикулярны друг другу  и имеют  ту           же частоту, то наличие интерференции зависит от

          <cos(ωt + φ1)cos(ωt + φ2)> = <1/2>= 12<cos                   (φ2 -φ1)>.

Здесь возможны 2 случая:

1)За время  усреднения сдвиг фаз изменяется  беспорядочно <cos(φ2 -φ1)>=0, интерференция отсутствует.

2)За время усреднения сдвиг фаз постоянен:

 <cos (φ2 -φ1)> = cos(φ2 -φ1), тогда результирующая интенсивность

             I = cos(φ2 – φ1).                                                                

Необходимое условие  существования  интерференции  можно  сформулиро- вать в другой форме:

Для возникновения  интерференции  необходимо,  чтобы разность фаз φ1 - φ2  сохраняла свое значение за время усреднения (т.е. колебания должны  быть коге-  рентны): Δφ = φ1 - φ2 = const.

Интерференция может наблюдаться, если колебания  являются  не  гармони-

ческими, когда фаза каждого из них является  какой-то функцией  времени и  они

являются не гармоническими, то интерференция может наблюдаться, если за  вре- мя усреднения разность  фаз  постоянна φ2(t) - φ1(t) = const.

Отсутствие интерференции  лучей, поляризованных во  взамно  перпендику-

лярных направлениях, было обнаружено Френелем и Араго в 1816 г.  и  интерпре-  тировано в 1817 г. Юнгом как доказательство поперечности световых волн.

Два гармонических колебания одной частоты всегда когерентны.

          Равенство частот интерферирующих  волн (ω1 = ω2) и неперпендикуляр- ность векторов  и  превращают необходимое условие  для  интерференции  в достаточное.

При разных частотах ω1 ω2 , как мы указывали, = 0. Если  же  час- тоты разные но близкие δω = ω1 -- ω2 ,, то интерференционная карти- на будет неустойчивой (биения).

Следует заметить, что совпадение  направлений  колебаний   и    двух плоскополяризованных волн вовсе не  означает  совпадение  направлений  колеба-

ний их магнитных векторов. Последние  совпадпют  только  в  случае, если обе

волны распространяются вдоль прямой. Но это не важно, т.к. световым  вектором  является вектор. В дальнейшем будем рассматривать только  одинаково направ-

ленные колебания.

Принято считать, что каждый цуг волн плоско поляризован. Однако для раз- личных цугов плоскости поляризации могут быть ориентирована по-разному.  По-         этому свет, излучаемый источником, представляет  собой  набор  плоскополяризо-  ванных волн со всевозможными направлениями E, удовлетворяющими только  ус-

ловию их перпендикулярности к лучу.

Таким образом и для двух пучков линейно поляризованного  света  при  ука- занном выше условии,  для  естественного  или  частично-поляризованного  света  будет  наблюдаться явление интерференции.

Говоря об интерференцинной картине, имеют  в  виду  устойчивую, не изме-

няющуюся со временем картину чередования min и max . Это  имеет место только

при условии когерентности или согласования волн.

Итак, результирующее колебание вектора в  точке наложения  двух  моно-

хроматических волн одинаковой частоты и линейно поляризованных в  одном  на-

правлении:

               , где

                      , и для интенсивности      

          При    ,

Если колебания синфазны, т.е. фазы φ1 и φ2   одинаковы  или  отличаются  на

четное число (т.е. Δφ = φ2 – φ1 = 2m, m = 0, ) т.е. cos(φ2 - φ1) = 1, то ин- тенсивность в этом случае max и равна

При  

Если колебания противофазны,  т.е.  фазы  φ1  и  φ2  отличаются  на  нечетное

число (Δφ = φ2 – φ1 = (2m + 1), m = 0, ), cos(φ2 - φ1) = -1, то  получается  min  интенсивность: . 

           При  I. min = 0.

          Если колебания  совершаются  в  квадратуре, т.е.  Δφ = φ2 – φ1 =m, m = = 0, ,  cos(φ2 - φ1) = 0, то

I = I1 + I2 – интесивность равна сумме интесивностей складываемых  колеба-

ний.

Способность когерентных волн к интерференции означает, что в любой  точ-

ке, которой достигнут эти волны, имеют  место  когерентные  колебания,  которые

будут интерферировать. Если разность фаз колебаний меняется от  одной  точки  к

другой, но в каждой точке области перекрытия не изменяется со временем, то ин-

терференция приводит к пространственному перераспределению энергии в облас-

ти перекрытия пучков, так что возникает устойчивая во времени интерференцион-

ная картина в виде чередующихся свелых и темных полос,  или  в  виде  череду- min  и  max.Результат интерференции (вид полос) определяется законом простран- ственного изменения  резкости фаз  интерферирующих  волн. А  разность  фаз  зависит от начальной разности фаз  источников, а  также  от разности  расстояний,  отделяющих точку наблюдения от источников каждой из волн.