Многолучевая интерференция. - Оптика. Лекции.

До сих пор при интерференции в тонких пленках мы рассматривали лишь двухлучевую интерференцию, возникающую в результате одного отражения от поверхностей пленки. Такое приближение дает хорошие результаты и является вполне оправданным, если коэффициент отражения на поверхностях пленки мал. При не очень малых R необходимо учитывать многократные отражения и рассматривать интерференцию в тонких пленках и пластинах как многолучевую.

В интерференционной картине от двух точечных одинаковых когерентных источников двухлучевой интерференции светлые и темные полосы имеют одинаковую ширину, причем переход от max к min происходит плавно, следуя закону. При разности фаз ,где m=0,±1,±2…Imax=4a2=4I0.

               Dj=(2m +1)p, m=0,±1,±2…Imin=0.

При остальных значениях j I имеет промежуточное значение. Полосы получаются размытыми, max не достаточно четко выделяются на общем фоне, что не выгодно для практических применений интерференции.

Многолучевая интерференция возникает при наложении большого числа когерентных световых пучков. Распределение интенсивности в интерференционной картине существенно отличается от двух лучевой интерференции.

Рассмотрим интерференцию, возникающую в плоскопараллельной пластине при прохождении плоской монохроматической волны.

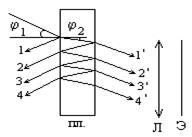Ранее мы пренебрегали вкладом в результирующую интенсивность пучков, испытавших более двух отражений (R  было мало). Теперь учтем лучи, претерпевшие многократные отражения.

Пусть d – толщина пластинки, n – показатель преломления, r и t - амплитудные и R=r2 и G=t2 – энергетические коэффициенты отражения и пропускания. Пусть коэффициент поглощения равен 0, значит R+Г =1. Если с обеих сторон пластинки находится одна и та же среда, то отражающая и пропускающая способность обеих границ пластинки будет одинакова.

При каждом прохождении через границу двух диэлектриков амплитуда волны изменяется в t раз, а при каждом отражении от такой границы она изменяется в r раз. Все лучи, выходящие из пластинки, порождены по методу деления амплитуды падающим лучом и являются когерентными. Они выходят из пластинки параллельным пучком и образуют локализованную в бесконечности интерференционную полосу равного наклона. Если на пластину падает рассеянный свет, то получим интерференционную картину полос равного наклона. Оптическая разность хода D каждых двух соседних интерферирующих лучей .

Т.к. с обеих сторон пластинки находится одна и та же среда, то в проходящем свете в результирующей D2',1' потери полуволны не будет.

Амплитуда результирующей прошедшей волны для длинной пластинки представится бесконечной убывающей геометрической  прогрессией. Записав сумму этой прогрессии, легко получить:  ,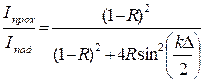

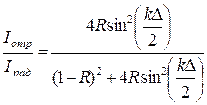 - формулы Эйри.

Линиям равных интенсивностей соответствует одно и то же значение угла j1, поэтому интерференционные полосы равного наклона в фокальной плоскости линзы имеют вид концентрических колец с центром в фокусе линзы. Центру картины соответствует наибольший порядок интерференции.

    при sin2(kD/2)=0   Þ   D=2dncosj2=ml

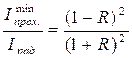      при sin2(kD/2)=1   Þ   D=2dncosj2=(2m+1)l/2.

Видность интерференционной картины в проходящем свете 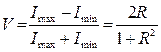. При R®1 V®1.

Положение max и min определяется точно теми же условиями, что и для двух лучевой интерференции. То же относится и к распределению интенсивности, если R<<1. Но распределение интенсивности I существенно изменяется при увеличении R, и особенно при R®1.

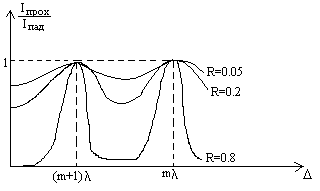Интенсивность в max в N2 раз больше, чем для одного пучка. N – число интерферирующих пучков. Т.е. в проходящем свете max становятся значительно ярче  (вследствие закона сохранения энергия Е увеличивается в N раз) и значительно уже.

Это позволяет для немонохроматического света легче разрешить max, принадлежащие различным l.

В отраженном свете – картина дополнительная – узкие темные линии на широком светлом фоне.

Многолучевая интерференция осуществляется в дифракционной решетке, а также в многолучевых интерферометрах: эталоне Фабри-Перо, пластинке Люммера-Герке. 

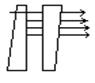    Интерферометр Фабри-Перо (1897г) является наиболее распространенным из интерференционных приборов высокого разрешения.

Состоит из двух стеклянных либо кварцевых пластинок, между которыми находится воздух. Плоские поверхности пластинок, обращенные друг к другу, тщательно отшлифованы и покрыты высокоотражающими покрытиями. При диэлектрическом покрытии R»98%. Отражающие поверхности строго параллельны друг другу. Наружные поверхности пластинок обычно образуют небольшие углы с внутренними, чтобы отраженный от них свет не мешал рассмотрению интерференционной картины.

Если d=0.5см, то mmax»20000. Чем выше порядок max, тем выше разрешающая способность прибора. Однако, чтобы полосы не перекрывались, необходимо работать со светом высокой монохроматичности: .

Интерферометр можно использовать для исследования тонкой структуры спектральных линий.

Интерферометр Люммера-Герке.

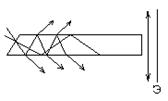Плоскопараллельная пластинка из очень однородного стекла или плавленого кварца со срезанным  концом.

Направление падающих лучей подбирается таким, чтобы на границе стекло-воздух угол был близок к углу полного внутреннего отражения.

Сейчас практически не применяется.

Эшелон Майкельсона.