В развитие идеи де Бройля о волновых свойствах частиц Шредингер в 1926 г. получил уравнение
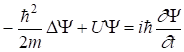 , (20)
, (20)
где m – масса частицы, ![]() – мнимая единица, U – потенциальная энергия частицы, D – оператор Лапласа .
– мнимая единица, U – потенциальная энергия частицы, D – оператор Лапласа .
Решение уравнения Шредингера позволяет найти волновую функцию Y(x,y,z,t) частицы, которая описывает микросостояние частицы и ее волновые свойства.
Если поле внешних сил постоянно во времени (т.е. стационарно), то U не зависит явно от t. В этом случае решение уравнения (20) распадается на два множителя
Y(x, y, z, t) =y(x, y, z) exp, (21)
где E/![]() =w.
=w.
В стационарном случае уравнение Шредингера имеет вид
![]() , (22)
, (22)
где Е, U – полная и потенциальная энергия, m – масса частицы.
Следует заметить, что исторически название "волновой функции" возникло в связи с тем, что уравнение (20) или (22), определяющее эту функцию, относится к виду волновых уравнений.
Поможем написать любую работу на аналогичную тему

