Спектр излучения атомарного водорода состоит из отдельных спектральных линий, которые располагаются в определенном порядке. В 1885 г. Бальмер установил, что длины волн (или частоты) этих линий могут быть представлены формулой. Действительно, из (7) с учетом (6) для водорода (Z = 1), следует, что
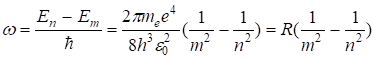, (8)
где R = 2,07× 1016 с -1 – постоянная Ридберга. Учитывая, что 1/l = v/с = w/2pс и используя (8), найдем
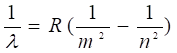, (9)
где R =1,0974×107 м-1 – называется также постоянной Ридберга.
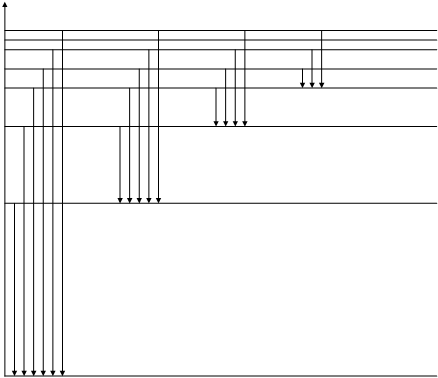
На рис. 1 изображена схема энергетических уровней атома водорода, рассчитанных согласно (6) при z = 1.
Еn, эВ
0 n = ¥
|
n = 4
|
|
СП
|
|||
|
|||
СБ
 |
|||
|
|||
СЛ
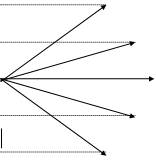
При переходе электрона с более высоких энергетических уровней на уровень n=1 возникает ультрафиолетовое излучение или излучение серии Лаймана (СЛ). Когда электроны переходя на уровень n = 2 возникает видимое излучение или излучение серии Бальмера (СБ). При переходе электронов с более высоких уровней на уровень n = 3 возникает инфракрасное излучение, или излучение серии Пашена (СП) и т.д.
Частоты или длины волн, возникающего при этом излучения, определяются по формулам (8) или (9) при m=1 – для серии Лаймана, при m=2 – для серии Бальмера и при m = 3 – для серии Пашена. Энергия фотонов определяется по формуле (7), которую с учетом (6) можно привести для водородоподобных атомов к виду:
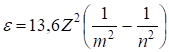, эВ (10)
Теория Бора сыграла огромную роль в создании атомной физики. В период ее развития (1913 – 1925 г.) были сделаны важные открытия, например, в области атомной спектроскопии. Однако в теории Бора обнаружились существенные недостатки, например, с ее помощью невозможно создать теорию более сложных, чем атом водорода, атомов. Поэтому становилось очевидным, что теория Бора представляет собой переходной этап на пути создания последовательной теории атомных и ядерных явлений. Такой последовательной теорией явилась квантовая (волновая) механика.
11.4 Атом водорода согласно квантовой механики. Квантовые числа электрона в атоме
Результаты, полученные согласно теории Бора в решении задачи об энергетических уровнях электрона в водородоподобных атомах, получены в квантовой механике без привлечения постулатов Бора. Покажем это.
Состояние электрона в водородоподобном атоме описывается некоторой волновой функцией y, удовлетворяющей стационарному уравнению Шредингера . Учитывая, что потенциальная энергия электрона
(11)
где r – расстояние между электроном и ядром, получим уравнение Шредингера в виде
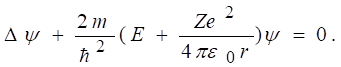(12)
Целесообразно воспользоваться сферической системой координат r, q, j и искать решение этого уравнения в виде следующих собственных функций
(13)
где n, l, m – целочисленные параметры собственных функций. При этом n – называют главным квантовым числом, l – орбитальным (азимутальным) и m – магнитным квантовым числом.
Доказывается, что уравнение (12) имеет решение только при дискретных отрицательных значениях энергии
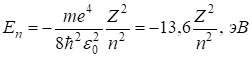, (14)
где n = 1, 2, 3,... – главные квантовые числа.
Сравнение с выражением (6) показывает, что квантовая механика приводит к таким же значениям энергии, какие получились и в теории Бора. Однако в квантовой механике эти значения получаются как следствие основных положений этой науки.
Подставив в (14 ) Z = 1 и приняв n = 1, получим значение энергии основного состояния (т.е. состояния с наименьшей энергией) атома водорода
эВ. (15)
Из решения (13) уравнения Шредингера (12) также следует, что момент импульса электрона в атоме квантуется по формуле
(16)
где l= 0, 1, 2, ... (n-1) – орбитальное (азимутальное) квантовое число.
Проекция момента импульса L электрона на направление
Z магнитного поля может принимать лишь целочисленные значения, кратные 
(пространственное квантование) т.е.
(17)
m – называют магнитным квантовым числом. При данном 
магнитное квантовое число может принимать 
различных значений.
|
|
 |
|||
 |
|||
l=1 l=2
Рис. 2
Первоначально предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Позднее было показано, что спин имеет квантовую природу. Спин следует считать внутренним свойством, присущим электрону, подобно тому, как ему присущ и заряд и масса.
Собственный момент импульса электрона LS (спин) выражается через спиновое квантовое число s равное 1/2, т.е. спин квантуется по закону
.
Проекция спина на заданное направление z может принимать два квантованных значения
,
где ms = ± s = ± 1/2 называют магнитным спиновым квантовым числом или просто спиновым квантовым числом, т.е. также как и s.
Поможем написать любую работу на аналогичную тему