Многим людям приходилось наблюдать радужную окраску мыльных пленок; цвета побежалости закаленных стальных деталей, покрытых тонким прозрачным слоем окисных пленок; тонких пленок нефти, бензина, масел, плавающих на поверхности воды. Все эти явления вызваны интерференцией света в тонких пленках.
Интерференцию света в тонких пленках можно наблюдать в проходящем или отраженном свете.
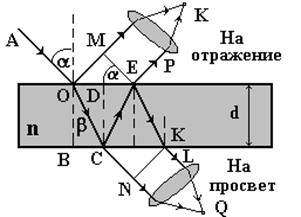
Рассмотрим интерференцию света на отражение от тонкой прозрачной пленки (пластинки) толщиной d с абсолютным показателем преломления n (рис. 2.5). Пластинка (пленка) находится в вакууме (n1 = nвак =1, l - длина волны света в вакууме, причем n > n1).
Пусть на пленку падает плоская монохроматическая волна l под углом a (луч АО). В т. О на верхней поверхности этот луч частично отражается (луч ОМ) и частично преломляется (луч ОС). Преломленный луч ОС, достигнув нижней поверхности пленки, в т. С испытывает, в свою очередь частичное отражение (луч СЕ) и преломление (луч СN), переходя снова в вакуум.
|
Рис. 2.5 |
Отраженный луч СЕ на верхней поверхности пленки в т. Е испытывает частичное отражение (луч ЕК) и частичное преломление (луч ЕР). Преломленный луч ЕР и отраженный луч ОМ когерентны и при наложении интерферируют. Действительно, если на их пути поставить собирательную линзу, то в т. К на экране можно наблюдать интерференционную картину на отражение, максимум и минимум которой будут определяться оптической разностью хода, возникающей между лучами ОМ и ЕР от точки 0 до плоскости ЕМ, т.е.
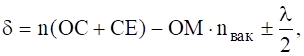(2.34)
где слагаемое 
возникает из-за потери полуволны при отражении света на границе раздела вакуум-пленка в. О. При n>n1=nвак данное слагаемое берут со знаком "-". Если же n<n1, то потеря полуволны произойдет в т. С и слагаемое 
необходимо брать со знаком "+".
Согласно рис. 2.5 ОС=СЕ=
, ОМ=ОЕsina=2dn×tgb×sina.
Применяя закон преломления
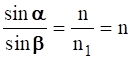, (n1=1) получаем после подстановки в (2.34) оптическую разность хода лучей на отражение 
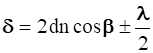(2.35)
или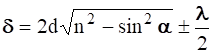 
. (2.36)
При dмах = 2m
максимум интерференции в тонких пленках на отражение удовлетворяет условию 
. (2.37)
При dmin = (2m+1)
получаем условие минимума интерференции в тонких пленках на отражение, т.е. 
. (2.38)
Аналогичный расчет можно провести для интерференции в тонких пленках на просвет в т. Q. Однако дополнительной оптической разности хода в этом случае не наблюдается.
Поэтому максимум интерференции в тонких пленках на просвет соответствует условию минимума на отражение - формула (2.38) и, наоборот, минимум интерференции в тонких пленках на просвет соответствует максимуму на отражение - формула (2.37).
При освещении пленки белым светом для некоторых длин волн будет выполняться условие максимума, а для других - условие минимума, поэтому пленка в отраженном свете выглядит окрашенной.
Поможем написать любую работу на аналогичную тему