Интерференция в тонких пленках. - Оптика. Лекции.

Не следует думать, что интерференцию света можно наблюдать только в лабораторных условиях, применяя для этого специальные оптические установки. В природе часто можно наблюдать радужное окрашивание тонких пленок (мыльные пузыри, масляные или нефтяные пленки на воде, пленки прозрачных окислов на поверхности старых стекол или так называемые цвета побежалости на поверхности металлов (для закаленных стальных деталей)). Все эти явления обусловлены интерференцией света в тонких прозрачных пленках, которая возникает в результате наложения когерентных волн, отражающихся от верхней и нижней поверхностей. Интерференционные полосы окрашены, т.к. свет белый. Явление интерференции в тонких пленках, наблюдаемое в естественных условиях при освещении их протяженными источниками света (напр. участок неба, т.е. рассеянный дневной свет) получило название цветов тонких пленок.

Как нами было уже показано, при интерференции двух волн от одного точечного источника появляется стационарная интерференционная картина, которая наблюдается на экране в любой области пространства, где  перекрываются интерферирующие пучки.

Поверхности постоянной разности фаз – гиперболоиды.

Наблюдаемая интерференционная картина называется нелокализованной (т.е. локализована всюду).

 В нашем случае, если пленка тонкая, то при точечном источнике апертура интерференции 2w будет очень малой, т.е. лучи света, идущие от источника к некоторой точке плоскости наблюдения, расходятся между собой на очень малые углы, и для образования интерференционной картины так же не требуется никакого фокусирующего устройства (например, опыт Поля).

Правда, если рассматривать интерференцию от точечного источника (падающая волна сферическая), как результат наложения лучей, полученных разделением одного и того же луча за счет отражения света от верхней и нижней поверхности пленки, то для наблюдения интерференции используется собирающая линза и экран.

При замене точечного источника протяженным область пространства, где может наблюдаться интерференция, ограничивается. Ведь четкие полосы будут наблюдаться только в том случае, если разность фаз для всех пар лучей, приходящих в данную точку из различных элементов источника света, одинакова или почти одинакова. В общем случае это условие удовлетворяется, если точка наблюдения лежит на некоторой определенной поверхности. Видны эти полосы, если глаз наблюдателя или оптический прибор наведены на эту поверхность.

Такие интерференционные полосы называют локализованными.

Необходимое условие локализации: при ширине d источника наблюдения интерференции в свете с длиной волны l возможно лишь в области пространства, где w удовлетворяет условию

Опыт с зеркалом Ллойда и привел к качественным соображениям о зависимости видимости интерференционной картины от апертуры интерференции, здесь же возник вопрос о локализации полос.

Наибольший интерес представляют случаи локализации интерференционных полос на поверхности какой-либо пластины (полосы равной толщины), и локализации их в бесконечности (полосы равного наклона).

Для установления общих закономерностей интерференции света в тонких пленках рассмотрим однородную плоскопараллельную прозрачную пластинку толщиной d, на которую падает под углом j, плоская монохроматическая волна (параллельный пучок света, т.е. источник света удален в бесконечность).

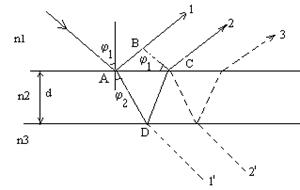Падающая волна, частично отражается от верхней поверхности пластинки, а частично преломляется. Преломленная волна частично отражается от нижней поверхности пластинки, частично преломляется. То же опять происходит на верхней поверхности. Формируется целая последовательность параллельных между собой пучков в отраженном и в проходящем свете. Интенсивность этих пучков различна. Если через  обозначить коэффициент отражения, а через  - коэффициент пропускания света на поверхности пластинки, то интенсивности рассматриваемых пучков можно представить в виде:

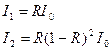
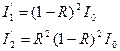          …   (1).

При n=1.5 в направлении нормали отражается »5% падающего светового потока (т.е. R=0.05). Тогда I1:I2:I3…=5%:0.25%:0.0125%…от I0. Поэтому будем рассматривать интерференцию только двух первых пучков. Вклад остальных пучков, вследствие их малой интенсивности, незначителен.

В результате имеем две когерентные волны с некоторой оптической разностью хода:

D2,1=n22AD-n1AB=n22(d/cosj2)-n1ACsinj1=2n2(d/cosj2)-n1sinj12dtgj2=2(d/cosj2)(n2-n1sinj1sinj2)=2d/cosj2(n2-n1(n2/n1)sinj2sinj2)=2(d/cosj2)n2(1-sin2j2)=2dn2cosj2.

.

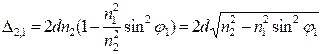
При расчете оптической разности хода нужно также иметь в виду, что световой вектор при отражении от границы раздела среды оптически менее плотной со средой оптически более плотной (с большим n) изменяет фазу на p (происходит потеря полуволны).

.

 в формуле может и не быть, если пластинка окружена сверху и снизу веществами с разной оптической плотностью, большей и меньшей, чем у нее (например, пленка воды на поверхности стекла).

Если n1=n3=1<n2, то  - в отраженном свете,

 в проходящем свете - .

Формула показывает, что все лучи, падающие на пленку под одним и тем же углом, разделяются на 2 когерентных луча и после отражений от поверхности пленки имеют одно и то же направление распространения, будучи параллельными друг другу. Между лучами, отразившимися от разных поверхностей пленки, возникает разность хода D, и они могут интерферировать.

Условие max: ,

                min: .

Зависимость D=f(d,j) имеет достаточно общий характер и ее можно применять и при описании возникновения как полос равного наклона, так и полос равной толщины.

Полосы равного наклона.

Условие точечности источника осуществляется лишь приближенно, а во многих случаях и совсем не выполняется. Часто приходится иметь дело с протяженными источниками при явлениях интерференции, наблюдаемых в естественных условиях, когда источником света служит участок неба, т.е. рассеянный дневной свет.

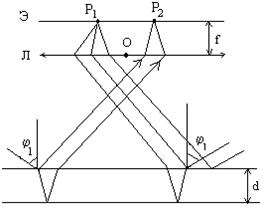Пусть на плоскопараллельную пластинку падает монохроматический пучок непараллельных лучей. В отраженном пучке будут присутствовать пары параллельных лучей различных направлений распространения, полученных отражением от верхней и нижней поверхностей пластинки.

Т.к. в каждой паре лучи параллельны друг другу (пластинка плоскопараллельная), то «пересекаются» они только в бесконечности, следовательно интерференционная картина локализована в бесконечности.

Для наблюдения интерференционных полос расположим параллельно пластинке линзу, в главной фокальной плоскости которой поместим экран.

  Можно также рассматривать интерференционную картину в подзорную трубу или глазом аккомодированным на бесконечность.

Лучи, лежащие в плоскости рисунка и падающие на пластинку под углом j1, после отражения от обеих поверхностей пластинки соберутся линзой в точках P1 и P2, имеющих одинаковую освещенность, определяемую значением оптической разности хода. Всякая линза обладает тем свойством, что она не создает дополнительной разности фаз между лучами, собираемыми линзой в одной и той же точке изображения. Лучи, идущие в других плоскостях, но падающие на пластинку под тем же углом j1, соберутся линзой в других точках, однако имеющих такую же освещенность. Таким образом, лучи, падающие на пластинку под одинаковым углом j1, создадут на экране совокупность одинаково освещенных точек, образующих определенную интерференционную линию. Аналогично, лучи, падающие под другим углом j1' создадут на экране другую совокупность одинаково (но иначе, поскольку D иная) освещенных точек. В результате на экране возникнет система чередующихся светлых  и темных полос.

  Каждая интерференционная линия определенной интенсивности соответствует определенному углу наклона образующих ее лучей к поверхности пластины. Поэтому такие интерференционные линии называются линиями равного наклона.

Каждая точка интерференционной полосы образована лучами, которые до прохождения линзы образуют параллельный пучок. Следовательно, полосы равного наклона локализованы в бесконечности.

Если пучок света, падающий на пластинку, аксиально-симметричен, то под каждым углом будет падать целый конус таких лучей и (в нашем случае, когда линза параллельна пластинке) и линии равного наклона являются концентрическими кольцами с центром в фокусе линзы.

При ином расположении линзы относительно пластинки (экран во всех случаях должен совпадать с фокальной плоскостью линзы) форма полос равного наклона будет другой.

В центре картины при j1=0° порядок интерференции максимален.

Если при перемещении пластинки параллельно самой себе ее толщина изменяется на видимом участке, то радиус интерференционных колец также изменяется, причем изменение его легко заметить при весьма незначительных изменениях толщины пленки. Это дает весьма эффективный способ контроля толщины пленки, широко используемый в производстве. Точность такого контроля очень большая, поскольку локальное изменение толщины пластинки на долю длины волны приводит к заметному невооруженным глазом изменению формы линии.

Посмотрим как влияют на четкость интерференционной картины размеры источника.

Каждая точка линии равного наклона есть результат интерференции лучей идущих от источника практически параллельными пучками. Таким образом, апертура интерференции в этом случае близка к нулю, следовательно, размеры источника могут быть достаточно большими.

Различные точки протяженного источника излучают некогерентно. Каждый элемент протяженного источника создает в фокальной плоскости линзы свою интерференционную картину. Однако картины эти (поскольку образованы параллельно падающими на пленку лучами) совершенно идентичны друг другу и не зависят от точки поверхности пленки, в которой произошло отражение. Положение полос в картинах совершенно одинаково и не зависит также от места элемента на источнике.

Накладываясь друг на друга, интерференционные картины усиливаются. Они будут столь же отчетливыми, как и с точечным источником. Следовательно, конечность размеров источника не смазывает картину интерференции линий равного наклона и не является ограничивающим интерференцию фактором. Увеличение размеров источника позволяет увеличить общую интенсивность интерференционной картины, сохраняя прежнюю резкость max и min. Т.к. все сказанное справедливо для одной вполне определенной плоскости наблюдения, то такая интерференционная картина локализована (в данном случае в бесконечности).

Тонкие пленки позволяют работать с протяженными источниками света. Но пока что мы говорили о строго монохроматическом излучении, порождаемом колебаниями вполне определенной частоты  . Но в реальных экспериментах используют источники, излучающие в достаточно широком интервале частот с той или иной степенью монохроматичности излучения.

Легко установить общую связь между степенью монохроматичности излучения и тем порядком интерференции, который можно наблюдать.

Условие исчезновения интерференции для света с l в интервале (l, l+Dl):

Интерференция не может наблюдаться, если max m-го порядка для (l+Dl) совпадает с max (m+1)-го порядка для излучения с длиной волны l, т.е. (m+1)l=m(l+Dl),

Порядок интерференционного max прямо связан с разностью хода D=ml, следовательно, 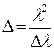,  чем больше разность хода (выше порядок интерференции), тем меньше должен быть интервал длин волн Dl, т.е. степень монохроматичности выше. Увеличение ширины линии излучения ухудшает видимость интерференционной картины.

Интерференционная картина будет стабильной во времени и отчетливой в пространстве, если соблюдены условия пространственной и временной когерентности.

Для того, чтобы имела место временная когерентность, разность хода не должна превышать длину когерентности .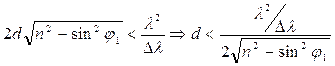

Выражение  имеет величину порядка 1 (для n=1,5 она изменяется от 1,12 при j1=90о до 1,5 при j1=0).

Следовательно,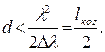

Таким образом, прошедшие или отраженные волны будут когерентными, если толщина пленки d не превышает величины, определяемой соотношением (…).

При увеличении толщины пленки видимость интерференционной картины ухудшается ввиду конечного значения временной когерентности.

Оценим допустимую толщину пленок для визуального наблюдения интерференции никак не монохроматизированного (естественного) света.

Согласно формуле для D положение max зависит от длины волны l. Поэтому в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных цветов, и интерференционная картина принимает радужную окраску.

Для наблюдения интерференции в белом цвете перекрытие полос от различных длин волн не должно смазывать цветовую гамму белого цвета. Средний глаз различает оттенки света длин волн, различающихся на мкм (100А°)

Пусть l=500нм, тогда , мкм.

Таким образом, для наблюдения интерференции в белом цвете толщина пленок должна быть достаточно малой. Поэтому речь идет об интерференции в тонких пленках, а не просто в плоскопараллельных пластинках.

При наблюдении интерференции от источника высокой монохроматичности, допустимая толщина пленки увеличивается. Например, ширина зеленой линии излучения ртутной лампы Dl=0,01нм, l=502,564нм, d»10мм.

В этих условиях не представляет труда наблюдать интерференционную картину со стеклянными пластинками толщиной в несколько см, которые используются в различных интерферометрах.

Для лазерного излучения длина когерентности составляет многие километры, следовательно, пластинки могут быть очень толстые. При увеличении толщины пластинки d или увеличении показателя преломления n расстояние между соседними max, т.е. ширина интерференционных полос, становится меньше.

Пространственная когерентность связана с размерами источника. Для наблюдения интерференции должно выполняться условие: , где l – размеры источника, 2w -  апертура интерференции.

Возвращаясь к способам наблюдения интерференционных полос разной локализации, будем считать, что пластины «тонкие», т.е. можно работать с протяженными источниками света, не применяя дополнительной монохроматизации.

Интерференция наблюдается не только в отраженном, но также и в проходящем сквозь пленку свете.

Оптические разности хода для лучей в отраженном свете и проходящем отличаются на l/2. Следовательно, интерференционные картины будут дополнительными (на месте min одной наблюдаются max другой и наоборот, т.е. одна из них смещена на полполосы по отношению к другой).

Кроме того, различным будет и качество картин. Согласно (1) при малом коэффициенте отражения (R»0.05) интенсивности отраженных лучей будут примерно одинаковы, хотя и небольшие. Поэтому интерференционные max наблюдаются на темном фоне.

Минимумы нулевые (формула ).

Проходящие же лучи сильно отличаются между собой по интенсивности, поэтому max наблюдаются на светлом фоне и видность картины низкая.

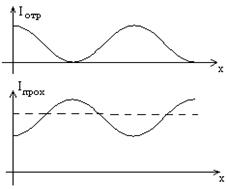
Если мы хотим рассматривать интерференционную картину в проходящем свете, надо взять пластинку с большим R.

Полосы равной толщины.

Если толщина пластинки переменна, то при освещении ее протяженным источником от различных участков ее поверхности пары лучей с одинаковой разностью фаз распространяются в разных направлениях и если поставить линзу и собирать на экране в фокальной плоскости отраженные от поверхности лучи, то каждая точка изображения образуется параллельными пучками. Каждый из таких пучков представляет совокупность лучей, отраженных от различных участков пленки, т.е. с разными значениями j1 и d. Следовательно, различные участки широких пучков будут иметь разные значения D. Следовательно, картина интерференции лучей равного наклона не возникает. Однако появляется другая интерференционная картина, локализованная на поверхности пластины.

Для ее наблюдения нужно аккомодировать глаз на верхнюю поверхность пленки. Если же мы хотим получить изображение интерференционной картины на экране, то собирающую линзу и экран нужно так расположить по отношению к пленке, чтобы на экране было видно изображение ее верхней поверхности.

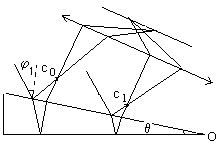
Пусть пластинка переменной толщины имеет вид плоского клина с углом при вершине q.

Если источник света находится на большом расстоянии от пластинки, лучи падают на ее поверхность почти под одним и тем же углом (т.е. падает фактически плоская волна).

  Лучи, отразившиеся от разных поверхностей клина, не будут параллельны. Они пересекаются в точках С1 и С2, лежащих в одной плоскости, проходящей через вершину клина О.

На рис. полосы локализованы над поверхностью. При другой конфигурации клина или угле падения могут быть мнимыми и локализованными и под клином.

При малом угле клина q разность хода для любой пары лучей можно с достаточной степенью точности вычислять по формуле, взяв в качестве d толщину пластинки в месте падения лучей.

, а  .

Разность хода для лучей, отразившихся от разных участков клина, не одинакова и определяется толщиной d. Освещенность экрана, проходящего через точки С1 и С2…, будет не равномерна. На экране появятся светлые и темные полосы.

Каждая из таких полос одинаковой освещенности возникает в результате отражения лучей от участков клина с одинаковой толщиной, вследствие чего их называют полосами равной толщины.

Для плоского клина полосы равной толщины представляют собой ряд интерференционных полос, параллельных ребру клина, на одинаковом расстоянии друг от друга l/2q. Если свет падает на нижнюю грань клина нормально, то полосы локализованы на верхней поверхности клина.

Контрастность интерференционной картины зависит от порядка интерференции, т.е. толщины пластинки (т.е. угла q).

При освещении клина немонохроматическим излучением от реального источника конечного размера отчетливость интерференционной картины уменьшается при перемещении от вершины клина к его основанию. Чем тоньше пленка, тем меньше апертура интерференции и лучше видимость полос.

Область локализации интерференционной  картины тем уже, чем меньше степень пространственной когерентности падающей волны.

Временная когерентность соблюдается при тех же ограничениях на толщину пластины, что и в случае линий равного наклона. При наблюдении в белом свете полосы будут окрашенными.

 Тонкая мыльная пленка, натянутая на вертикально расположенный каркас, дает интерференционную картинку в виде полос равной толщины. Такие полосы можно наблюдать в тонкой прослойке между двумя поверхностями двух прозрачных пластинок. Этим пользуются для испытания качества оптических поверхностей при их шлифовке, где в качестве одной из плоскостей – исследуемая, другой – эталон, точность – 0.1l и менее. Также для измерения малых углов между двумя поверхностями.

Таким образом, сопоставим два рассмотренных нами случая интерференции при отражении от тонких пленок. Полосы равного наклона получаются при освещении пластинки постоянной толщины (d=const) рассеянным светом, в котором содержатся лучи разных направлений. Локализованы полосы равного наклона в бесконечности.

Полосы равной толщины наблюдают при освещении пластинки непостоянной толщины параллельным пучком света (j=const). Локализованы полосы равной толщины вблизи пластинки. В реальных условиях (например радужные цвета на мыльной пленке) наблюдаются полосы смешанного типа (так как изменяется и d, и j).