Дифракционная решетка - Материалы для подготовки к экзамену по физике. Оптика.

Дифракционная решетка - высококачественный  спектральный прибор, представляющий собой совокупность большого числа регулярно расположенных одинаковых параллельных друг другу щелей шириной а, разделенных непрозрачным промежутком b, нанесенных на плоскую или вогнутую (выпуклую) поверхность. Применяется  для разложения излучения в спектр, определения  длины волны света и пр.

Решетка характеризуется периодом d=a+b, числом щелей на единицу длины n=1/d и общим числом щелей N. Общая длина решетки L=Nd.

Различают амплитудные и фазовые дифракционные решетки.

У амплитудной дифракционной решетки периодически изменяется коэффициент отражения или пропускания, что приводит к изменению амплитуды падающей волны.

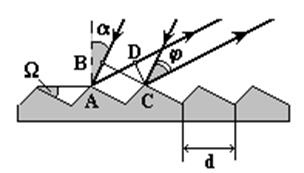
У фазовой дифракционной решетки штрихи имеют специальную (например, треугольную) форму, которая изменяет фазу световой волны (рис. 3.5).

Если на плоскую отражательную решетку падает световая волна в виде параллельного пучка лучей, то в результате интерференции когерентных лучей от всех N  штрихов решетки пространственное (по углам) распределение интенсивности света можно представить в виде произведения двух функций: J=JN×J1.

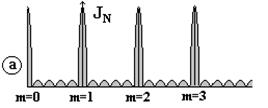
Функция J1 определяет интенсивность света при дифракции на одном штрихе (рис. 3.6, б). Интенсивность  JN обусловлена интерференцией N когерентных лучей от всех штрихов решетки.

Для данной длины волны l функция JN определяется периодом d, полным числом штрихов N, углами падения a и дифракции j и не зависит от формы штрихов,

т.е.

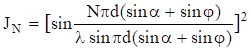. (3.19)

Оптическая разность хода между когерентными параллельными лучами, падающими под углами j от соседних штрихов фазовой отражательной дифрак- ционной решетки,   

                                               d= АВ+СD =d(sina+sinj).                                    (3.20)

Функция JN есть периодическая, с регулярной интенсивностью главных максимумов и вторичными максимумами малой интенсивности (рис. 3.6, а).

Между соседними главными максимумами располагаются N-2 вторичных максимума и N -1 минимум.

 Положение главного максимума определяется из условия

                                                  sin                                                (3.21)

или                                      (m=1, 2, 3,...).                                    (3.22)

Таким образом условие максимума определяется уравнением решетки

                                            d=d(sina+sinj) = ± ml.                                 (3.23)

Следовательно, главные максимумы возникают в направлениях, если оптическая разность хода между соседними когерентными пучками равна целому числу длин волн.

Интенсивность всех главных максимумов одинакова:  JNmax = N2.             (3.24)

Функция J1 зависит от d, l, a, j, от формы штриха и определяется по формуле (3.16).

Следовательно, интенсивность максимумов дифракционной решетки можно рассчитать по формуле 

                       J =N2× J1.                         (3.25)

Интенсивность для данного угла   дифракции j дифракционной решетки найдем по формуле

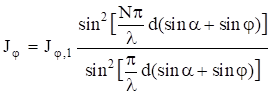  .        (3.26)

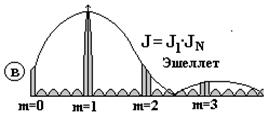
Фазовую  дифракционную решетку с треугольным профилем штриха, концентрирующую около 80% энергии светового потока при m¹0 (обычно m=1 или m=2) называют эшеллетом. Угол, под которым происходит концентрация падающего светового потока в спектре, называют углом блеска. Изменяя угол наклона штриха грани, можно совместить центральный дифракционный максимум функции J1 с любым интерференционным главным максимумом функции JN  любого порядка, кроме m¹0 (рис. 3.6, в).

При этом углы a и jмах должны одновременно удовлетворять соотношению (3.23)

                                                       a + j=2W.                                               (3.27)

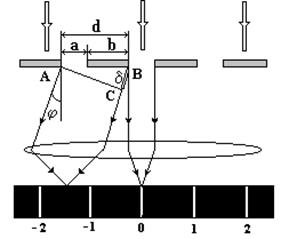
При нормальном падении монохроматического света на прозрачную дифракционную решетку на экране возникает дифракционная картина (рис. 3.7), для которой условие максимума принимает вид   

                                                           d=d sinj = ± ml.                   (3.28)

Действительно, если для расчета дифракционной картины использовать метод зон Френеля, то  каждую щель разделим на z зон.

Если в каждой щели укладывается четное число зон z, то на экране возникает минимум, для которого справедливо условие минимума для одной щели (3.14). Если в каждой щели укладывается нечетное число зон, то каждая из них  становится точечным источником монохроматического света.

В этом случае расчет дифракционной картины решетки сводится к задаче о расчете интерференционной картины от многих когерентных источников с постоянной разностью фаз  ( метод щелей Юнга).

Например, при   dмin= (2m+1), получаем условие минимума для дифракционной решетки:  dsinj = (2m+1) .        (3.29)

При  dмах= 2m - условие максимума для дифракционной решетки, формула  (3.28).

Угловое положение m-го главного максимумам интенсивности дифракционной прозрачной решетки при нормальном падении света на нее определяется условием                                             sinjm, max.                                             (3.30)

Кроме минимумов, определяемых условием      sinjk, min,              (3.31)

между двумя соседними главными максимумами располагаются N-1 добавочных минимумов, угловые направления которых определяются условием

                                                   sinj,                                                            (3.32)

 где k принимает целочисленные значения, кроме 0, N, 2N, 3N, ..., kN.

Основными спектральными характеристиками дифракционной решетки являются угловая дисперсия  , разрешающая способность R и область дисперсии  Dl.

1. Угловая дисперсия характеризует степень пространственного разделения лучей с разной длиной волны.

После дифференцирования (3.23) или (3.28)  имеем  .          (3.33)

2. Разрешающая способность дифракционной решетки   R=               (3.34)

или                                          R=mN=,                                     (3.35)

где dl - минимальная разность длин волн двух монохроматических линий l и   l+ dl равной интенсивности, которые еще можно  различить в спектре, L=Nd - длина решетки.

В этом случае используют критерий Рэлея: две спектральные линии разрешены, если  центральный максимум одной из них совмещен с первым минимумом другой.

3. Область дисперсии дифракционной решетки Dl=l2 - l1 - величина интервала спектра, при котором спектр данного порядка m не перекрывается со спектром соседних порядков. Область дисперсии определяется из условия

                                            d (sina+ sinjmax)=ml2=(m+1) l1,                               (3.36)

т.е.             или .

Из уравнения решетки следует, что угол дифракции главных максимумов

 jмах =f(l). Следовательно, дифракционная решетка пространственно по углам разлагает излучение различных длин волн и на экране возникает одновременно несколько спектров для каждого значения m¹0 (величину m=0, 1, 2, ... называют порядком спектра). При m=0 разложения в спектр не происходит, т.к. условие d(sina+sinj)=0 справедливо для всех длин волн. При этом j = - a, т.е. направление на максимум нулевого порядка определяется зеркальным отражением от плоскости решетки. Следовательно, падающий и дифрагирующий пучки нулевого порядка располагаются симметрично относительно нормали к решетке. По обе стороны от направления на максимум нулевого порядка расположены максимумы и спектры m = ±1, m = ±2, ... порядков.