Решетка имеет N щелей и расстояние d=a+b называется периодом решетки.
Световой эффект от дифракции на решетке можно найти сложив действие всех N щелей. Для этого удобно использовать комплексную форму световых волн. В этом случае это будет ряд, представляющий геометрическую прогрессию
![]() (15)
(15)
Здесь d разность фаз определяемая разностью хода ![]() , а Δ=dsinφ. Дробь
, а Δ=dsinφ. Дробь![]() можно представить в виде
можно представить в виде 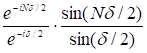 , где
, где ![]() – есть мнимая часть. Учитывая, что
– есть мнимая часть. Учитывая, что 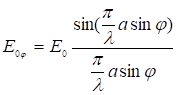 и введя обозначение
и введя обозначение ![]() и
и ![]() , выражение для действительной части колебаний запишется в виде
, выражение для действительной части колебаний запишется в виде 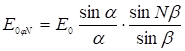 (16) Выражение для интенсивности будет
(16) Выражение для интенсивности будет
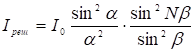 (17)
(17)
Множитель ![]() определяет действие одной щели, а множитель
определяет действие одной щели, а множитель 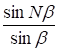 определяет взаимодействие N щелей.
определяет взаимодействие N щелей.
Условие главных максимумов dsinφ=mλ (18) дает для ![]() , следовательно
, следовательно 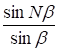 и максимальная амплитуда будет NЕ0j. Амплитуда главных максимумов модулируется множителем (sina/a). Максимальное значение этого множителя равно 1 и достигается при a=0, т.е. j=0, соответствующее центральному максимуму. Минимумы достигаются когда в результате сложения комплексных амплитуд, получается результирующая нулевая амплитуда. Для различных d (т.е. при различных j) ломаная кривая при векторном сложении может быть замкнута много раз, это удовлетворяется при разности фаз волн от крайних щелей равной 2p, 4p… . Поэтому условие минимумов в дифракционной картине запишется в виде Nδ=2πm (m=0, 1, 2,…) учитывая
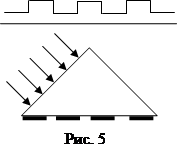
и максимальная амплитуда будет NЕ0j. Амплитуда главных максимумов модулируется множителем (sina/a). Максимальное значение этого множителя равно 1 и достигается при a=0, т.е. j=0, соответствующее центральному максимуму. Минимумы достигаются когда в результате сложения комплексных амплитуд, получается результирующая нулевая амплитуда. Для различных d (т.е. при различных j) ломаная кривая при векторном сложении может быть замкнута много раз, это удовлетворяется при разности фаз волн от крайних щелей равной 2p, 4p… . Поэтому условие минимумов в дифракционной картине запишется в виде Nδ=2πm (m=0, 1, 2,…) учитывая ![]() (19), имеем dsinφ=(m/N)λ; m¹0, N, 2N… В виду того, что в решетке ширина щели a обычно мала, то центральный максимум довольно широк, так что на его протяжении укладывается несколько главных максимумов решетки (Рис. 4). Если решетка включает периодические изменения в амплитуду волны, не влияя на нее сразу, то ее называют амплитудной. Если же решетка вносит периодические изменения в фазу волны, но не влияет на ее амплитуду, то ее называют фазовой. Амплитудной решеткой служить решетка, представляющая собой совокупность равностоящих щелей в непрозрачном экране. Приближением фазовой решетки может служить стеклянная пластинка с периодически изменяющейся толщиной (рис. 5), отражательной фазовой решеткой может служить призма с преломляющим углом 900
на гипотенузной стороне которой напылены равностоящие полоски серебра параллельно преломляющему ребру. Свет отражается от посеребренных и непосеребренных полосок, при этом фаза волны изменяется по-разному. Амплитуда волны при отражении не меняется.
(19), имеем dsinφ=(m/N)λ; m¹0, N, 2N… В виду того, что в решетке ширина щели a обычно мала, то центральный максимум довольно широк, так что на его протяжении укладывается несколько главных максимумов решетки (Рис. 4). Если решетка включает периодические изменения в амплитуду волны, не влияя на нее сразу, то ее называют амплитудной. Если же решетка вносит периодические изменения в фазу волны, но не влияет на ее амплитуду, то ее называют фазовой. Амплитудной решеткой служить решетка, представляющая собой совокупность равностоящих щелей в непрозрачном экране. Приближением фазовой решетки может служить стеклянная пластинка с периодически изменяющейся толщиной (рис. 5), отражательной фазовой решеткой может служить призма с преломляющим углом 900
на гипотенузной стороне которой напылены равностоящие полоски серебра параллельно преломляющему ребру. Свет отражается от посеребренных и непосеребренных полосок, при этом фаза волны изменяется по-разному. Амплитуда волны при отражении не меняется.
 Трехмерные, пространственные решетки обладают периодичностью в трех различных направлениях. Обозначим периоды d1, d2, d3.
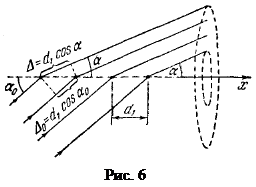
Найдем условие образования дифракционных максимумов. В качестве таких решеток являются кристаллические. Сначала рассмотрим действие отдельной цепочки с периодом d1 (рис. 6). Угол падения
Трехмерные, пространственные решетки обладают периодичностью в трех различных направлениях. Обозначим периоды d1, d2, d3.
Найдем условие образования дифракционных максимумов. В качестве таких решеток являются кристаллические. Сначала рассмотрим действие отдельной цепочки с периодом d1 (рис. 6). Угол падения
a0, δ0=2πΔ0/λ, Δ0=d1cosα0, Δ=d1cosα (20)
 Усиление будет при
Усиление будет при
d1(cosα-cosα0)= ±mλ (21)
Каждому значению m соответствует свой конус. Условие для другого направления с периодом d2 будет аналогично
d2(cosβ-cosβ0)= ±mλ (22)
и для d3
d3(cosγ-cosγ0)= ±mλ
Эти условия называются формулами Лауэ. Наибольшее значение модуля разности косинусов равно 2. поэтому эти условия могут быть выполняемы при отличном от нуля значениях индекса m лишь в том случае, если l не превышает 2d. В случае прямоугольной системы координат углы a, b, g связаны друг с другом следующим образом
cos2α+ cos2β+ cos2γ=1 (23)
 Система уравнений (21, 22, 23) будет разрешимой лишь для некоторых определенных длин волн. Каждому такому значению l соответствует только один максимум. Русский ученый Вульф и английские физики Брэгги показали, что расчет дифракционной картины от кристаллической решетки можно осуществить простым способом.
Система уравнений (21, 22, 23) будет разрешимой лишь для некоторых определенных длин волн. Каждому такому значению l соответствует только один максимум. Русский ученый Вульф и английские физики Брэгги показали, что расчет дифракционной картины от кристаллической решетки можно осуществить простым способом.
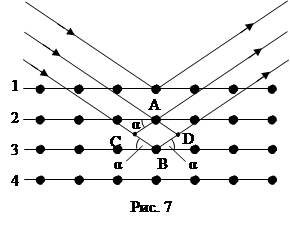
Рассмотрим дифракцию рентгеновских лучей на кристаллической решетке (рис. 7). a – угол скольжения луча с атомной плоскостью. Разность хода между двумя лучами при отражении будет
CB=BD=dsinα, (24)
общая разность хода Δ=2dsinα, а условие максимума
2dsinα=кλ (25)
Эта формула называется формулой Вульфа-Брегга.
Поможем написать любую работу на аналогичную тему

