Согласно квантовой теории электрон в металле не имеет точной траектории, его можно представить волновым пакетом с групповой скоростью, равной скорости электрона. Квантовая теория учитывает движение электрона в периодическом поле решётки, что приводит к появлению эффективной массы электрона 
. Расчёт, выполненный на основе этого, приводит к формуле
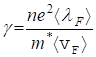, (4)
которая по внешнему виде напоминает классическую формулу (3). Здесь n - концентрация электронов проводимости в металле, álFñ - средняя длина свободного пробега электрона, имеющего энергию Ферми, ávFñ - средняя скорость теплового движения такого электрона.
Разгоняться в электрическом поле могут только электроны, энергия которых близка к уровню Ферми , т. е. в проводимости участвует малая часть электронов, импульс которых m*<vF> близок к импульсу электрона на уровне Ферми PF
, т. е. m*<vF> 
. С учётом этого из (4) следует, что g ~ álFñ.
Увеличение температуры приводит к возрастанию тепловых колебаний кристаллической решётки, на которых рассеиваются электроны (на квантовом языке говорят о столкновении электронов с фононами), и длины свободного пробега электрона álFñ~ 1/s ~ 
. Здесь 
- площади “сечения” колеблющихся атомов решётки, а - амплитуда колебания. Она связана с температурой 
~ 
. Следовательно, álFñ ~ 
~ 
и удельная электропроводность g ~ álFñ ~ 1/T, что согласуется с экспериментом.
Таким образом, квантовая теория объяснила электропроводность металлов. 
Поможем написать любую работу на аналогичную тему