Циклотронное вращение

Рассмотрим движение в постоянном однородном магнитном поле. Уравнение движения частиц имеет вид:

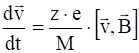                                     .                                            (2)

Как было уже сказано, движение заряженной частицы в постоянном магнитном поле может быть представлено как наложение движения вдоль поля и циклотронного (ларморовского) вращения поперёк поля с циклической частотой:

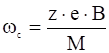                                        .                                               (3)

Эта частота называется циклотронной или ларморовской.

Так как:

                                  ,
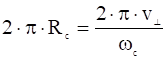то:

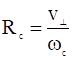                                           ,                                                  (4)
 называется циклотронным радиусом. Если в поле частицы совершают тепловое движение, то циклотронные радиусы будут распределены так же, как и скорости теплового движения.

Медленное изменение внешних условий называется адиабатическим. Качественно условие адиабатичности сводится к требованию, чтобы относительное изменение магнитного поля было малым: во времени – за период циклотронного вращения; в пространстве — на длине, равной циклотронному радиусу:

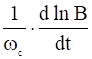
                                      ,                                             (5)

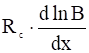
                                      .                                             (6)

Циклотронное вращение проявляется в полной мере только в разреженной плазме, где столкновения между частицами редки. В плотной плазме столкновения происходят часто, и кулоновские взаимодействия нарушают правильное циклотронное вращение. Для того, чтобы циклотронное вращение могло проявиться, нужно, чтобы период его был мал в сравнении со временем между столкновениями или, точнее, средним временем  передачи импульса вследствие взаимодействий между частицами плазмы. Поскольку период вращения обратно пропорционален частоте, то это условие можно записать так:

                                           .                                                  (7)
Плазму, удовлетворяющую этому условию, называют замагниченной. В замагниченной плазме тепловое движение поперёк поля имеет характер циклотронного вращения. Если условие замагниченности не соблюдается, то, не успев закончить циклотронный оборот, частица сбивается с траектории в результате изменения направления движения, вызванного столкновениями.

Условие замагниченности можно представить и в другом виде. Введём длину свободного пробега  в отсутствие магнитного поля:

                                           .
Тогда условие замагниченности можно записать в виде:

                                             ,                                                    (8)
то есть циклотронный радиус должен быть мал по сравнению с длиной свободного пробега.

Так как  (см. формулу (1)), то плазму можно сделать замагниченной, наложив на неё достаточно сильное магнитное поле. Сделать это тем легче, чем больше время передачи импульса , то есть чем реже столкновение и слабее взаимодействие между частицами.

В замагниченной плазме в полной мере проявляется анизотропия проводимости и других процессов переноса. Напротив, проводимость можно считать скаляром, если выполняется условие:

                                           ,                                                 (9)
обратное условию замагниченности. При этом условие (9) полностью применимо к приближению магнитной гидродинамики с конечной проводимостью.

Если плазма ограничена в пространстве, то циклотронное вращение может возмущаться не только столкновениями частиц между собой, но и конечными размерами системы. В этом случае кроме условия (7) должно быть выполнено ещё и второе условие замагниченности: циклотронный радиус мал в сравнении с размерами системы, то есть:

                                            .                                                 (10)

Отметим, что дрейфовое движение является следствием циклотронного вращения. Для того, чтобы движение имело дрейфовый характер, требуется выполнение двух условий:

1)  условия адиабатичности;

2)  условия замагниченности.

Условие замагниченности (7) можно записать как:  ( – частота передачи импульса). Ввиду того, что циклотронная частота у ионов в тысячи раз меньше, чем у электронов, условие замагниченности для электронов осуществляется гораздо легче. Если условие (7) выполняется как для электронов, так и для ионов, то все частицы плазмы участвуют в дрейфовом движении. Возможны случаи, когда , то есть электроны замагничены, а ионы – нет. В этом случае в дрейфовом движении принимают участие только электроны.

В случае идеальной проводимости  (или ). Таким образом, если выполнено условие идеальной проводимости, то условие замагниченности заведомо выполняется, то есть движение имеет дрейфовый характер.