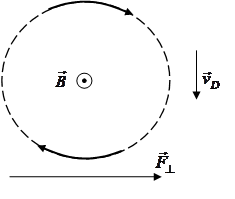
Чтобы просто и наглядно представить природу дрейфового движения и оценить величину дрейфовой скорости, рассмотрим циклотронную окружность. Сила ![]() , действующая поперёк магнитного поля, в одной половине циклотронного периода действует вдоль направления вращения, в другой – против этого направления. Как видно из рисунка, в верхней половине окружности сила действует по направлению вращения, в нижней – против. В результате частица будет двигаться сверху вниз быстрее, чем снизу вверх. Разность этих скоростей приведёт к смещению циклотронной окружности с постоянной скоростью
, действующая поперёк магнитного поля, в одной половине циклотронного периода действует вдоль направления вращения, в другой – против этого направления. Как видно из рисунка, в верхней половине окружности сила действует по направлению вращения, в нижней – против. В результате частица будет двигаться сверху вниз быстрее, чем снизу вверх. Разность этих скоростей приведёт к смещению циклотронной окружности с постоянной скоростью ![]() в направлении, перпендикулярном как магнитному полю, так и действующей силе. Это смещение и называется дрейфом. Оценим величину скорости дрейфа. Сила
в направлении, перпендикулярном как магнитному полю, так и действующей силе. Это смещение и называется дрейфом. Оценим величину скорости дрейфа. Сила ![]() создаёт ускорение
создаёт ускорение ![]() . За время
. За время ![]() циклотронного периода приращение скорости
циклотронного периода приращение скорости ![]()
![]()
![]() . В рассмотренном примере скорость вращения в направлении вниз будет на величину такого порядка больше, вверх – меньше средней. Разность этих скоростей даёт скорость дрейфа, величина которой:
. В рассмотренном примере скорость вращения в направлении вниз будет на величину такого порядка больше, вверх – меньше средней. Разность этих скоростей даёт скорость дрейфа, величина которой:
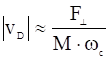 , (11)
, (11)
или, если подставить значение циклотронной частоты:
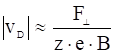 . (12)
. (12)
При оценке множители порядка единицы опущены. Чтобы указать не только величину, но и направление дрейфовой скорости, нужно записать её выражение в векторной форме. Векторное выражение для дрейфовой скорости можно получить из уравнения (1), приняв, что ![]() , где
, где ![]() – скорость циклотронного вращения, удовлетворяющая уравнению:
– скорость циклотронного вращения, удовлетворяющая уравнению:
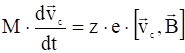 . (13)
. (13)
Скорость ![]() медленно меняется со временем, так что производной её по времени можно пренебречь. Тогда для дрейфовой скорости:
медленно меняется со временем, так что производной её по времени можно пренебречь. Тогда для дрейфовой скорости:
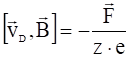 .
.
Умножение векторно справа на ![]() даёт:
даёт:
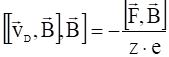 ,
,
или:
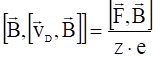 .
.
Раскрывая двойное векторное произведение, получим:
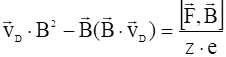 .
.
Если скорость ![]() перпендикулярна
перпендикулярна ![]() , то второе слагаемое слева обращается в ноль, и получим:
, то второе слагаемое слева обращается в ноль, и получим:
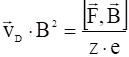 ,
,
или:
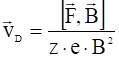 .
.
Поможем написать любую работу на аналогичную тему

