Ранее проводимость 
вводилась как феноменологическая характеристика плазмы. Чтобы найти её значение и выяснить физический смысл, необходимо кроме движения плазмы как целого учесть также относительное движение электронов и ионов. Это делается в более детальной модели двух "жидкостей": электронной и ионной, движущихся одна сквозь другую. Электрическое сопротивление плазмы рассматривается при этом как результат взаимного трения этих двух "жидкостей".
Запишем уравнение движения электронов и ионов в виде, аналогичном уравнению (2), считая, что на электроны действует только электронное давление 
, на ионы – только ионное давление 
. Взаимное трение, то есть передачу импульса при взаимодействии между частицами, учтем введением сил трения 
и 
, которые должны удовлетворять третьему закону Ньютона. Удобнее писать уравнения не для скорости, а для импульса. Тогда движение электронов и ионов будет описываться в гидродинамическом приближении системой уравнений:
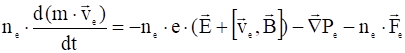, (9)
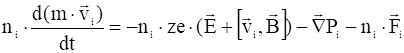. (10)
Сила трения , испытываемая электронами, пропорциональна концентрации ионов (
), а сила трения , испытываемая ионами, – концентрации электронов (
). Представим эти силы как произведения коэффициента вязкого трения 
на разность скоростей и на концентрации тормозящих частиц. Тогда уравнения (9) и (10) примут вид:
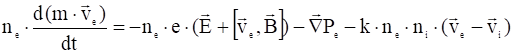, (11)
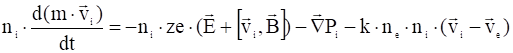. (12)
Плазма удовлетворяет условию квазинейтральности:
, или 
. (13)
Плотность тока:
. (14)
Из (13) и (14) можно получить, что:
.
Если сложить уравнения (11) и (12) с учетом (13) и (14), то силы электрического поля и трения уничтожаются. Уничтожение электростатических сил является следствием квазинейтральности, уничтожение сил трения – следствием третьего закона Ньютона. В результате получится уравнение магнитной гидродинамики (2), в котором роль скорости течения плазмы 
играет среднемассовая скорость:
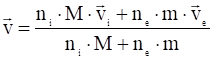. (15)
Пренебрегая массой электронов в сравнении с массой ионов, можно считать, что 
.
В этом приближении из (14) скорость электронов:
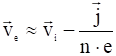. (16)
Рассмотрим более подробно силы трения. Из законов механики следует, что передача импульса при взаимодействии пропорциональна приведённой массе 
взаимодействующих частиц:
.
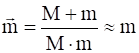Представим коэффициент трения в виде:
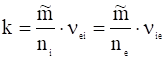. (17)
Определим размерность величин и 
:
, 
;
, 
.
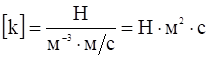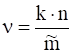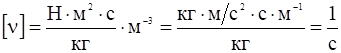Величины имеют размерность частоты. Это эффективные частоты передачи импульса от электронов к ионам и от ионов к электронам. По аналогии с кинетикой нейтральных частиц, где передача импульса происходит при столкновениях, величины часто называют эффективными частотами столкновений.
Из (17) следует, что 
.
Величину, обратную , называют временем передачи импульса:
.
С учетом (16) и (17) уравнения движения принимают вид:
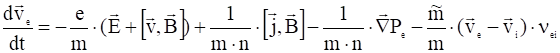, (18)
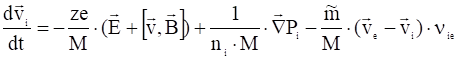, (19)
в этом уравнении членом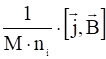 
следует пренебречь.
Отметим, что 
можно рассматривать как электрическое поле в сопутствующей системе координат, движущейся со средней массовой скоростью плазмы.
Чтобы иметь полную систему макроскопических уравнений модели двух жидкостей, нужно кроме уравнения для массовой скорости получить уравнение для плотности тока, которое называют обобщенным законом Ома. В общем случае получение этого уравнения осложняется тем, что лагранжевы производные содержат нелинейные члены:
.
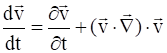Простые формы обобщенного закона Ома могут быть получены для двух случаев:
1) стационарного, когда производные по времени вообще равны нулю;
2) для колебаний малой амплитуды, когда можно пренебречь нелинейными членами и заменить лагранжевы производные на частные производные по времени (линейные колебания).
Если пренебречь членами вида 
, вычесть первое уравнение из второго и отбросить члены, содержащие в знаменателе массу 
(то есть пренебречь ускорением ионов), то с учетом равенства получим обобщенный закон Ома в виде:
,
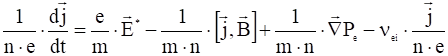или:
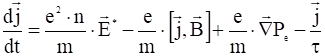, (20)
при этом величина 
в уравнении (20) есть время передачи импульса от электрона к ионам:
.
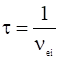Уравнения (2) и (20) образуют полную систему уравнений модели двух жидкостей.
Поможем написать любую работу на аналогичную тему