Проводимость плазмы

Для простейшего случая постоянного тока в однородной плазме уравнение обобщенного закона Ома (20) принимает вид:

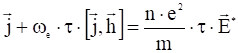                           ,                                (22)

где 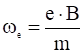 – электронная циклотронная частота:

 – единичный вектор в направлении магнитного поля.

При отсутствии магнитного поля или для составляющей тока вдоль его направления векторное произведение  обращается в нуль, и из уравнения (22) получится продольная составляющая проводимости плазмы:

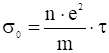                                        .                                             (23)

Для нахождения поперечной проводимости расписываем уравнение (22) в составляющих. Если направить ось z вдоль магнитного поля, то:

                                ,

                                .

Поперечная проводимость плазмы есть величина тензорная, то есть:

                         ,

                         ,

                         ,

или:

                                       .

Чтобы найти компоненты этого тензора, достаточно умножить одно из уравнений на , прибавить ко второму или вычесть из него, чтобы получить:

                     ,

                     .

Отсюда тензор проводимости однородной плазмы для постоянного тока имеет вид:

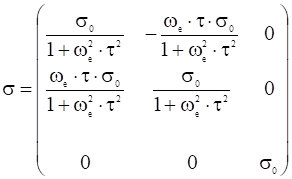                     .                          (24)

В явном виде составляющие плотности тока выражаются формулами:

                              ,

                              ,

                                         .

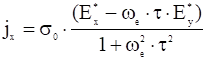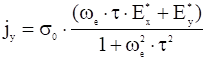Отметим, что если  – большое число, то в этом случае поперечная проводимость должна быть гораздо меньшей продольной и уменьшаться обратно пропорционально квадрату циклотронной частоты, то есть квадрату индукции магнитного поля. Ток должен течь не только вдоль электрического поля, но и поперек него (холл-эффект). В реальных условиях проводимость плазмы сильно осложняется пространственной неоднородностью, вызывающей электрическое поле поляризации, а также дрейфовые токи и ток намагничивания.