Приближение идеальной проводимости

Во многих задачах от приближения магнитной гидродинамики можно перейти к ещё более упрощенному способу рассмотрения плазмы, устремив проводимость  к бесконечности. Такое приближение носит название приближения идеальной проводимости. При бесконечной проводимости сколь угодно малое электрическое поле вызывало бы бесконечно большой ток, что требовало бы бесконечно большой затраты энергии, и поэтому невозможно. Следовательно, в приближении идеальной проводимости электрическое поле в системе координат, связанной с плазмой, должно равняться нулю:

                                   ,                                        (25)

откуда:

                                         .

Векторное произведение  зависит только от составляющей скорости, перпендикулярной к магнитному полю . Поэтому можно записать, что:

                                        .                                             (26)

Таким образом, условие (25) накладывает определенное требование на скорость движения плазмы поперек магнитного поля ; скорость вдоль магнитного поля  может иметь любое значение. Чтобы получить значение , достаточно умножить (26) векторно на  справа. Получим:

                ,

так как скалярное произведение . Таким образом, имеем:

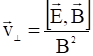                                         .                                              (27)

В скрещенных магнитном и электрическом полях идеально проводящая среда должна двигаться со скоростью, определяемой формулой (27). Такое движение называется дрейфом. Существует несколько разновидностей дрейфа, но только для дрейфа в скрещенных магнитном и электрическом полях скорость дрейфа одной частицы совпадает со скоростью плазмы в целом. Этот вид дрейфового движения называется электрическим дрейфом.