Колебания в холодной плазме

Холодной называется плазма, у которой газовое давление мало по сравнению с магнитным:

                                      .

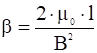
Если это условие выполнено, то при рассмотрении большинства вопросов, относящихся к колебаниям плазмы, можно полностью пренебречь тепловым движением и рассматривать только усредненное движение под действием внешних полей. Будем пренебрегать также столкновениями и всеми процессами, приводящими к затуханию колебаний, то есть к диссипации энергии.

Теория колебаний холодной плазмы заключается в совместном рассмотрении уравнений движения проводящей среды и уравнений Максвелла.

Применяя операцию  к обоим частям уравнения:

                                        ,

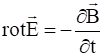получим:

                                   .

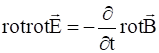Подстановка уравнения:

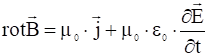
даёт:

                        .

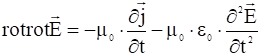Раскрывая операцию  по формулам векторного анализа, приходим к результату:

                     .

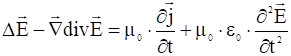В плоской волне любая величина  зависит от координат и времени как:

                             ,

где  – комплексная амплитуда.

Фазовая скорость волны 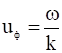, групповая скорость 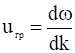. В анизотропных средах частоты связаны не только с величиной, но и с направлением волнового вектора, то есть дисперсионное уравнение имеет вид:

                                   ,

где , и  – составляющие волнового вектора.

В линейном приближении уравнения для комплексных амплитуд  имеют такой же вид, что и для величин . Для плоской волны имеем:

                                 , ;

                                      , .

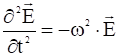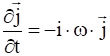Тогда можно записать:

              .                     (1)

При рассмотрении линейных колебаний лагранжеву производную  можно заменить частной  и в произведении  пренебречь собственным полем волны , то есть заменить  на постоянное внешнее магнитное поле . Уравнение движения плазмы принимает вид с учетом сделанных допущений:

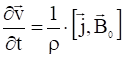                                      .                                             (2)

Обобщенный закон Ома запишем в виде:

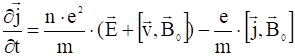                     .                            (3)

Система уравнений (2) и (3) совпадает с системой уравнений магнитной гидродинамики для идеального проводника, из которых выброшены силы давления. В соответствии с этим приближение холодной плазмы называют иногда гидродинамическим приближением.

Введём характерные частоты:

- плазменную частоту ,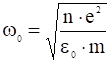

- циклотронные частоты    .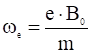

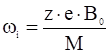Если не пренебрегать массой электрона по сравнению с массой иона, то плазменная частота определяется так:

                                       ,

где , .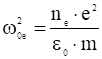

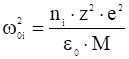Учитывая условие электронейтральности , получим:

                                .

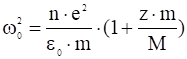Эта величина настолько мало отличается от электронной плазменной частоты, что в дальнейшем не будем их различать. Тогда:

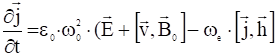                       ,                              (4)

где  – единичный вектор в направлении магнитного поля.

Рассмотрение и описание всех типов колебаний в холодной плазме сводится к совместному решению системы уравнений (1), (2) и (4). При выводе этой системы сделаны следующие допущения:

1) плазму считаем полностью ионизованной;

2) амплитуды всех переменных величин в волне полагаются малыми, чтобы можно было пренебречь всеми квадратичными членами (линейное приближение);

3) тепловое (газовое) давление считается малым по сравнению с магнитным давлением (приближение холодной плазмы);

4) пренебрегаем всеми диссипативными процессами (приближение идеальной плазмы;

5) отбрасываются члены порядка отношения массы электрона к массе иона. Это допустимо, если приближение проведено аккуратно в математическом отношении.