Кажущаяся простой система векторных уравнений оказывается в действительности для произвольного направления распространения волн довольно громоздкой.
Рассмотрим сначала несколько простых случаев:
а) при распространении волны поперек магнитного поля или при распространении вдоль магнитного поля, как показывает анализ, колебания с электрическим полем, поперечным магнитному, отщепляются, то есть представляют собой независимые ветви колебаний. Магнитное поле на эти ветви колебаний не действует.
Для колебаний с электрическим полем, параллельным магнитному полю, когда 
, выполняется условие 
. Это значит, что колебания, поляризованные вдоль магнитного поля и распространяющиеся продольно, представляют собой электростатические плазменные колебания.
Для волн, распространяющихся поперек магнитного поля, не поляризованных вдоль него, дисперсионное уравнение имеет вид:
.
Эта ситуация тождественна рассмотренной при отсутствии магнитного поля.
Рассмотренные типы колебаний, поляризованные вдоль магнитного поля и распространяющиеся вдоль и поперек него, являются единственными, на которые магнитное поле в приближении холодной плазмы не действует.
б) Магнитогидродинамические волны.
Рассмотрим волны, распространяющиеся вдоль магнитного поля при произвольном направлении поляризации. Такую волну можно разложить на две независимые волны, у одной из которых электрическое поле параллельно, а у другой – перпендикулярно к магнитному. Волна, у которой как направление распространения, так и направление поляризации параллельны внешнему магнитному полю, в холодной плазме вырождается в плазменные колебания фиксированной частоты 
.
Перейдём теперь к волне, распространяющейся вдоль магнитного поля, но поляризованной поперёк него. Для этой волны 
, тогда:
. (*)
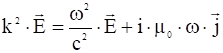Рассмотрим сначала предельную область очень низких частот 
. Для этой области получается очень простое дисперсионное уравнение:
,
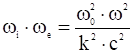откуда фазовая скорость волны:
,
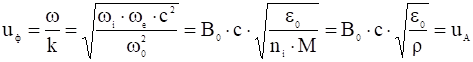где 
– плотность плазмы.
Такие волны называются альфвеновскими или магнитогидродинамическими, а скорость 
– альфвеновской скоростью.
Пренебрегая током смещения, то есть членом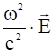 
в уравнении (*), запишем:
,
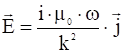то есть 
.
Предельная область полностью описывается уравнением магнитной гидродинамики, и формулу для легко получить из модели идеально проводящей области. Запишем линеаризованное уравнение движения:
;
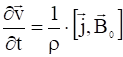или:
.
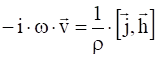Следовательно:
.
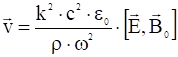Используя далее условие идеальной проводимости 
, и учитывая, что 
, получим дисперсионное уравнение:
,
,
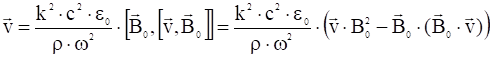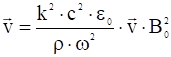или:
.
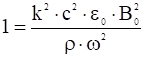Тогда фазовая скорость:
.
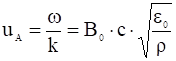Условие обеспечивает вмороженность магнитного поля.
Рассмотрим физическую картину магнитогидродинамических волн. Они могут рассматриваться как поперечные колебания силовых линий вместе с плазмой, в которую они вморожены. В области низких частот (), магнитогидродинамические волны распространяются с поперечной скоростью, то есть дисперсия отсутствует и групповая скорость равна фазовой.
Чтобы можно было пренебречь током смещения, необходимо, чтобы 
. Преобразуем это условие к виду:
,
то есть магнитная энергия плазмы должна быть мала по сравнению с энергией поля. При малой плотности плазмы или очень сильном магнитном поле это условие может не выполняться. В этих случаях простое дисперсионное уравнение должно быть заменено более сложным соотношением. Если для волн, распространяющихся вдоль магнитного поля, условие не выполняется, то возникает дисперсия и проявляются гиротронные свойства плазмы. Дисперсионное уравнение имеет вид:
.
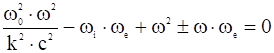Для квадрата показателя преломления плазмы получим:
,
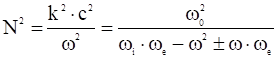откуда следует, что при двух частотах, обращающих в ноль знаменатель, 
. Эти частоты называются резонансными (или частотами аномальной дисперсии). Частоты аномальной дисперсии равны электронной и ионной циклотронным частотам. Особенностью таких волн является круговая поляризация, поэтому их называют волнами с круговой поляризацией. Двум знакам в дисперсионном уравнении отвечают две волны, вращающиеся в противоположных направлениях. Одна из них называется обыкновенной волной. У обыкновенной волны электрический вектор вращается в том же направлении, как и отрицательный заряд в магнитном поле.
Суперпозицией двух волн, поляризованных по кругу в противоположных направлениях, можно получить линейно поляризованную волну. Но в области 
способны распространяться только необыкновенные волны и, следовательно, линейная поляризация невозможна. При частотах ниже ионной циклотронной, но близких к ней, обыкновенная и необыкновенная волны распространяются с разными скоростями и, следовательно, линейно поляризованная волна расщепляется на две волны с круговой поляризацией. Но при частотах скорости распространения обыкновенной и необыкновенной волн различаются настолько мало, что расщепление линейно поляризованной волны происходит очень медленно, поэтому приближенно оно может быть описано как медленное вращение плоскости поляризации (эффект Фарадея). В связи с этим применительно к области низких частот () говорят о магнитогидродинамических волнах, которые могут быть поляризованы произвольным образом в плоскости, перпендикулярной к направлению распространения.
Волны с круговой поляризацией (геликоны) имеют существенное значение в физике ионосферы, где они проявляются в виде низкочастотных радиопомех.
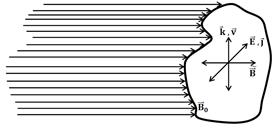
Рассмотрим структуру волн с круговой поляризацией.
 |
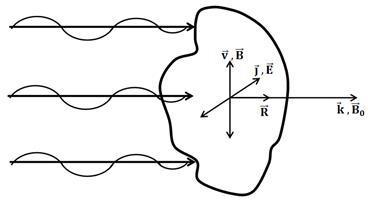Анализ показывает, направление тока 
совпадает с направлением электрического поля волны , то есть . Скорость движения вещества 
всегда перпендикулярна как направлению внешнего магнитного поля, так и направлению тока в волне, то есть движение вещества происходит в плоскости, перпендикулярной к направлению распространения и под углом 900 к направлению тока и электрического поля, то есть вдоль направления переменного магнитного поля волны 
.
Волны, распространяющиеся вдоль внешнего магнитного поля, имеют круговую поляризацию. Это относится и к полям, и к токам, и к скорости движения вещества плазмы.
С уменьшением частоты вращение векторов вокруг направления внешнего магнитного поля замедляется и в пределе получается магнитогидродинамическая волна.
в) Рассмотрим волны, распространяющиеся перпендикулярно к внешнему магнитному полю. В этом случае волна, поляризованная вдоль поля, отщепляется, поэтому будем рассматривать волны, у которых поляризация перпендикулярна к внешнему магнитному полю. Такие волны имеют уже эллиптическую поляризацию.
Рассмотрим область очень низких частот . В этом случае эллиптическая поляризация вырождается в линейную поляризацию. Дисперсионное уравнение имеет приближенный вид:
,
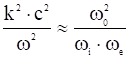что совпадает с уравнением для магнитогидродинамических волн.
 |
Таким образом, при очень низких частотах волны в плазме распространяются как параллельно к магнитному полю, так и перпендикулярно с одной и той же альфвеновской скоростью, однако структура этих волн различна.
Для волн, распространяющихся поперёк магнитного поля, структура следующая. Если направить ось z вдоль внешнего магнитного поля, а ось x – вдоль направления распространения волны, то ток и электрическое поле волны направлены по оси y, а гидродинамическая скорость – по оси x. Таким образом, волна является поперечной в электродинамическом смысле, но продольной в гидродинамическом. Переменное магнитное поле волны 
параллельно внешнему магнитному полю 
. Процесс колебаний можно рассматривать как периодическое сжатие и расширение плазмы вместе с вмороженным в неё магнитным полем. По физическому механизму этот процесс аналогичен распространению звука, вследствие чего он и называется магнитным звуком.
При частотах скорость распространения магнитного звука не зависит от частоты аналогично обычной акустике. Эту область малых частот называют магнитоакустической областью. При частотах порядка и выше ионной циклотронной при том же механизме возникает дисперсия. В этой области частот волны остаются магнитнозвуковыми, но не являются уже магнитоакустическими.
При рассмотрении дисперсии магнитного звука необходимо найти частоты аномальной дисперсии. Частоты аномальной дисперсии магнитного звука при распространении точно поперёк магнитного поля называют гибридными частотами 
. Верхняя гибридная частота определяется выражением:
,
её иногда называют электронно-плазменной гибридной частотой.
Вторая гибридная частота приближённо равна (
):
.
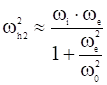Если 
, то:
.
При уменьшении плотности плазмы возникает довольно широкая промежуточная область, в которой выполнены неравенства 
.
В этой области:
.
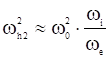Более общий результат при условии 
имеет вид:
.
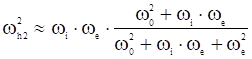Вторая гибридная частота зависит в основном от электронной и ионной циклотронных частот, вследствие чего её называют электронно-ионной гибридной частотой. Если плазма содержит несколько сортов ионов, то возникают ещё ион-ионные гибридные частоты, каждая из которых лежит между двумя ионными циклотронными частотами.
При приближении к гибридной частоте наблюдается дисперсия: показатель преломления возрастает, а фазовая скорость уменьшается. При частотах выше электронно-ионной гибридной частоты магнитно-звуковые волны не могут проникать в холодную плазму точно поперёк магнитного поля. При ещё более высоких частотах поперечное распространение вновь становится возможным вблизи электронно-плазменной гибридной частоты, то есть в области электромагнитных волн. Волны, распространяющиеся точно вдоль или поперек постоянного внешнего магнитного поля, называют прямыми. Для общего случая волн, распространяющихся под произвольным углом к внешнему магнитному полю (косые волны), приходится использовать тензорные соотношения.
Отметим, что в области, где поперечное распространение запрещено, магнитный звук может распространяться в виде косых волн, то есть малое отклонение от строго поперечного направления распространения снимает ограничения, наложенные гибридной частотой.
Поможем написать любую работу на аналогичную тему