Ковариация. Выборочный коэффициент парной корреляции

Основная задача корреляционного анализа заключается в выявлении взаимосвязи между случайными переменными путём оценки коэффициентов корреляции и детерминации, а также проверки значимости полученных значений.

            В эконометрике корреляционный анализ применяется для отбора факторов, оказывающих наибольшее влияние на исследуемый показатель и оценки качества построенных эконометрических моделей.

            Мерой взаимосвязи между двумя переменными v и w является выборочная ковариации, вычисляемая по правилу:

,

где  - результаты наблюдений, n – число наблюдений,  Обозначения переменных специально выбраны отличные от x и y, чтобы подчеркнуть возможность наличия связи между двумя любыми переменными, не обязательно являющимися объясняющей и объясняемой переменными.

            Существенным недостатком ковариации является зависимость от единиц, в которых измеряются переменные v и w. Если мы одни и те же данные запишем с использованием различных единиц измерения, то получим различные значения ковариации. То есть любое ненулевое значение ковариации само по себе не позволяет сделать вывод о тесноте связи между переменными.

            Поэтому для измерения силы связи между двумя переменными используется парный коэффициент корреляции. Парный коэффициент корреляции является показателем тесноты связи между переменными v и w лишь в случае линейной зависимости между этими переменными.

            В практических расчётах обычно используется выборочный парный коэффициент парной корреляции, определяемый по имеющемуся набору фактических данных:

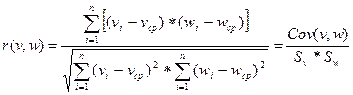        ,                                   (2.1)

где - выборочные значения дисперсии переменных v и w.

            Парный коэффициент корреляции обладает следующими свойствами:

1)      принимает значение в интервале , то есть ;

2)      не зависит от выбора начала отсчёта и единицы измерения ,

где a, b, c, d – постоянные величины, причём a и с – положительны;

3)      если , то между переменными имеется прямая связь, то есть при возрастании (убывании) одной из них другая также возрастает (убывает); если , то связь является обратной, то есть при возрастании одной переменной другая убывает;

4)      если , то между переменными имеется функциональная линейная зависимость, а если , то линейная связь между переменными отсутствует; соответственно, чем ближе модуль коэффициента парной корреляции к единице, тем теснее связь между переменными.

Заметим, что при отсутствии линейной связи между двумя переменными, между ними может существовать тесная связь другого вида.

            Пример 1.  В таблице приведены данные об объёмах продаж мороженого в магазине за день y, в зависимости от температуры воздуха в городе x2 и процента торговой надбавки x3. Видно, что спрос быстро растёт при повышении температуры воздуха. При наступлении очень высоких температур, предприятие резко увеличивает наценку, поскольку оказывается не в состоянии физически удовлетворить резко возрастающий спрос и сдерживает его повышением цен.

Требуется определить наличие между переменными линейных корреляционных связей, сделать выводы об их тесноте и охарактеризовать как прямые или обратные.

                                                                                                            Таблица 1.

            Решение. В первую очередь вычислим средние значения переменных в предложенной выборке данных:. Аналогично, . Тогда выборочные коэффициенты парной корреляции:

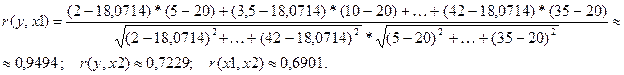
Следовательно, мы можем сказать, что между переменными y (объём продаж) и x1 (температура воздуха) имеется тесная прямая линейная связь. Между переменными x1 (температура воздуха) и x2 (торговая наценка) также наблюдается тесная прямая линейная зависимость. То же самое можно сказать о взаимосвязи между переменными y и x2.

            Для того, чтобы проверить, можем ли мы делать вывод о наличии линейной корреляционной связи между переменными по полученному значению коэффициента парной корреляции производится оценка его значимости, то есть определяется действительно ли полученное значение отражает наличие линейной связи, или же ненулевое значение коэффициента получено в результате случайных колебаний показателей или является следствием погрешности в вычислениях.