Проверка значимости параметров парной линейной модели

            Поскольку в результате наблюдений мы имеем случайные значения yi, то и вычисленные с их помощью параметры парной линейной модели a и b также являются случайными величинами. Для оценки надёжности полученных значений a и b производится проверка их значимости с использованием стандартной ошибки оценки, которая, в свою очередь, определяется по значениям ряда остатков εi:

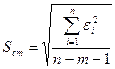,                                                      (2.6)

где n – количество наблюдений, m – количество факторных переменных в модели. Выражение (2.6) для определения стандартной ошибки оценки будет использоваться нами в дальнейшем неоднократно, поскольку применимо в случае нелинейных моделей, а также при наличии в модели двух и более факторных переменных, то есть является универсальным.

            Собственно проверка значимости параметров линейной модели производится в три этапа, аналогично тому, как это делалось для проверки значимости выборочного коэффициента корреляции.

            На первом этапе вычисляются t –статистики:

,                                                     (2.7)

где

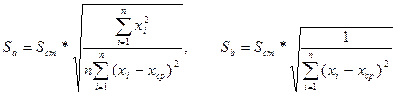.                                (2.8)

            На втором этапе определяется критическое значение tкр(α;n-m-1) по таблицам или с помощью функции СТЮДРАСПОБР в Excel. Уровень значимости α задаётся, а число степеней свободы вычисляется по числу наблюдений n и числу факторов m (в парной модели фактор x единственный).

                Наконец, на третьем этапе вычисленные значения t-статистик сравниваются с критическими значениями tкр. Если расчётное значение больше табличного, то соответствующий параметр (коэффициент уравнения) считается значимым. В противном случае коэффициент значимым не является, то есть его можно положить равным нулю.

             Произведём проверку значимости линейной модели парной регрессии, которую мы построили по данным Примера 1. Стандартная ошибка оценки вычисляется по значениям ряда остатков линейной модели εi ( приведён в последней колонке Таблицы 2):

.

Тогда, с использованием результатов вычислений из Таблицы 2, получаем:

При уровне значимости 10% и числе степеней свободы 7-1-1=5 имеем tкр=2,02. Поскольку расчётные значения t-статистик для обоих параметров больше критического значения, то с вероятностью 90% можно утверждать, что оба параметра линейного уравнения - а и b являются значимыми.