Для оценки параметров a и b линейной парной регрессии с использованием имеющегося набора результатов наблюдений наиболее часто используют метод наименьших квадратов (МНК), который минимизирует сумму квадратов εi - отклонения результатов наблюдений yi от рассчитанных по линейной модели (2.3) значений yрi:
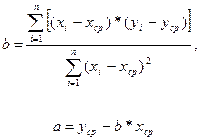(2.5)
Такое решение может существовать только при выполнении условия 
, то есть когда не все наблюдения проводились при одном и том же значении факторной переменной (сумма квадратов равна нулю, если каждое слагаемое равно нулю). Это условие называется условием идентифицируемости модели.
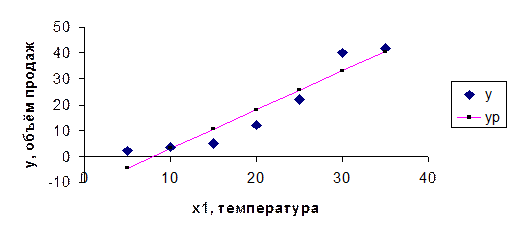
По данным, приведённым в Примере 1, построим линейную модель для объёма продаж мороженного y в зависимости от температуры воздуха x1. Промежуточные данные вычислений и модельные значения yр приведены в Таблице 2.
Таблица 2.
|
x1 |
y |
x1i-x1ср |
yi-yср |
(x1i-x1ср)2 |
(x1i-x1ср)*(yi-yср) |
yр |
ε |
|
|
|
5,0 Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
2 |
-15,0 |
-16,07 |
225,00 |
241,07 |
-4,43 |
6,43 |
|
|
10,0 |
3,5 |
-10,0 |
-14,57 |
100,00 |
145,71 |
3,07 |
0,43 |
|
|
15,0 |
5 |
-5,0 |
-13,07 |
25,00 |
65,36 |
10,57 |
-5,57 |
|
|
20,0 |
12 |
0,0 |
-6,07 |
0,00 |
0,00 |
18,07 |
-6,07 |
|
|
25,0 |
22 |
5,0 |
3,93 |
25,00 |
19,64 |
25,57 |
-3,57 |
|
|
30,0 |
40,0 |
10,0 |
21,93 |
100,00 |
219,29 |
33,07 |
6,93 |
|
|
35,0 |
42,0 |
15,0 |
23,93 |
225,00 |
358,93 |
40,57 |
1,43 |
|
Сумма |
140,0 |
126,5 |
0,0 |
0,00 |
700,00 |
1050,00 |
126,50 |
0,00 |
|
Среднее |
20,0 |
18,1 |
b= |
1,5 |
a= |
-11,93 |
|
|
 |
|
Исходные данные наблюдений и результаты расчётов приведены на следующем рисунке Рис 1. Модель парной линейной регрессии
Таблица и график построены средствами табличного процессора Excel.
Таким образом уравнение парной линейной модели имеет вид:
.
Поможем написать любую работу на аналогичную тему