Уравнение регресси, его смысл и назначение. Выбор типа математической функции при построении уравнения регресси.

Пусть мы располагаем n парами выборочных наблюдений над двумя переменными X и Y: X1, …, Xn; Y1, …, Yn

    Функция f(X) называется функцией егресси Y по X, если она описывает изменение условного среднего значения результирующей переменной Y в зависимости от изменения значений объясняющей переменной X:f(X)=E(Y |X).

уравнение регрессионной связи между Y и X имеет вид

     Yi =f(Xi)+ui, i=1,…,n,          (2.2)

    u – случайная величина (случайный член, возмущение), обусловленная источниками:

l Ошибки спецификации: не включение важных объясняющих переменных,  агрегирование переменных, неверная функциональная зависимость.

l Ошибки измерения при сборе исходных данных; использование аппроксимирующих переменных для учета факторов, непосредственное измерение которых невозможно.

Допущения модели (2.2)

1. E(ui)=0, i=1,…,n.

      Нет систематического смещения у u.

      Возьмем в (2.2) матожидание от обеих   частей при фиксированном значении X, получим: E(Y|X) =E(f(X))+E(u), по свойству матожидания Þ  E(Y|X) =f(X)+E(u), а поскольку с учетом определения функции регрессии должно быть f(X)=E(Y |X), то необходимо E(u)=0.

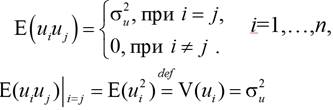
2. т.е. дисперсия случайной компоненты постоянна (независимо от того, при каких значениях объясняющей переменной производятся наблюдения i) - гомоскедастична.

, т.е. связь между значениями случайного члена для любых двух наблюдений отсутствует (независимость друг от друга ui и uj).

3.    X1, …, Xn – неслучайные величины.

задача регрессии имеет вид:

Yi =f(Xi)+ui, i=1,…,n,

при ограничениях

E(ui)=0, i=1,…,n.                                        (2.3)

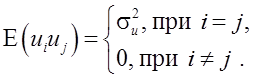                          (2.4)

X1, …, Xn – неслучайные величины.        (2.5)

Выбор вида функции в (2.2)

l используется априорная информация о содержательной экономической сущности анализируемой зависимости – аналитический способ,

l предварительный анализ зависимости с помощью визуализации – графический способ,

l использование различных статистических приемов обработки исходных данных и экспериментальных расчетов.