Спецификация уравнения регрессии: ошибки спецификации

Нередко на четвёртом этапе приходится констатировать, что оценённая модель неадекватна объекту-оригиналу. Это значит, что на этапе спецификации модели, вероятно, допущены какие-то ошибки. Чаще всего они содержатся в спецификации переменных в уравнении регрессии. Вот типичные ошибки такого вида:

üневерно выбран тип функции, играющей роль уравнения регрессии в модели с одной объясняющей переменной;

ü в линейное уравнение множественной регрессии включена лишняя объясняющая переменная;

üв линейное уравнение множественной регрессии не включена значимая объясняющая переменная.

Неверный выбор уравнения парной регрессии («а»)

Пусть на первом этапе экономист составил спецификацию модели парной регрессии (15.1):

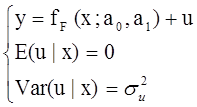
с ошибочно выбранным уравнением регрессии: yR= fF (x;a0,a1)

линейным по коэффициентам (а0, а1)

Предположим, что истинное уравнение регрессии у на х задаётся такой функцией: yR= fT (x;a0,a1) при которой:fT (x;a0,a1)- fF (x;a0,a1)=φ(x)≠0  (15.4)

Это значит, что E(u|x)= fT (x;a0,a1),

но в силу условия (15.4) E(u|x)≠ fF (x;a0,a1).(15.6)

Из неравенства (15.6) следует, что предпосылка Е(у|х)=0,  (15.7)

принятая в спецификации (15.1), ложна, так как на самом деле справедливо иное соотношение:

Е(у|х)=E(y- fF (x;a0,a1)| x)= Е(у|х) - fF (x;a0,a1)|= φ(x)≠0  (15.8)

Итак, последствием ошибочного выбора функции в качестве уравнения регрессии является нарушение предпосылки 15.7 о нулевом ожидаемом значении случайного возмущения. В итоге МНК-оценки коэффициентов модели оказываются смещёнными, и их среднеквадратические ошибки уже не являются объективными характеристиками точности. В конечном счёте, прогноз (точечный и интервальный) значения у0 эндогенной переменной у, вычисленный при х = хо оценённой модели оказывается неадекватным.

Симптомы ошибки:

üнесоответствии диаграммы рассеяния, построенной по выборке, графику функции.

üдлительное постоянство знака у смежных значений оценок случайных возмущений

üразительное отличие одноимённых коэффициентов в двух оценённых вариантах модели

В линейное уравнение множественной регрессии включена лишняя объясняющая переменная («б»)

Пусть на первом этапе экономист составил спецификацию модели множественной регрессии

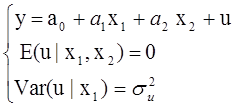 (15.16)

в ситуации, когда одна из объясняющих переменных, скажем, х2, является лишней, но экономист об этом не знает и оценивает МНК параметров по выборке: (a0, a1,a2;σu2) модели, где а2=0.

Результат: МНК-оценки параметров:   не имеют смещения, однако их точность не является максимально возможной, ошибка «б» способна привести экономиста к выводу, что оценённая модель неадекватна.

В линейном уравнении множественной регрессии пропущена значимая объясняющая переменная («в»)

Ошибка этого типа противоположна ошибке типа «б» эквивалентна по последствиям и симптомам ошибке типа «а» Следовательно, все последствия и симптомы ошибки типа «а» без каких-либо изменений переносятся и на данную ошибку.