Предположим, что по данным выборочной совокупности была построена линейная модель множественной регрессии. Рассмотрим процесс проверки значимости коэффициента множественной корреляции. Основная гипотеза состоит в предположении о незначимости коэффициента множественной корреляции, т. е.
![]()
Обратная гипотеза состоит в предположении о значимости коэффициента множественной корреляции, т. е. Н1:R(y,xi)≠0.
Данные гипотезы проверяются с помощью F-критерия Фишера через коэффициент множественной детерминации. Наблюдаемое значение F-критерия (вычисленное на основе выборочных данных) сравнивают со значением F-критерия, которое определяется по таблице распределения Фишера, и называется критическим.
При проверке значимости коэффициента множественной корреляции критическое значение F-критерия определяется как Fкрит(a;k1;k2 ), где а – уровень значимости, k1=l–1 и k2=n–l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров.
При проверке основной гипотезы вида Н0:R(y,xi)=0 наблюдаемое значение F-критерия Фишера-Снедекора рассчитывается по формуле:
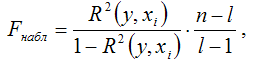
где R2(y,xi) – коэффициент множественный детерминации.
При проверке основной гипотезы возможны следующие ситуации.
Если Fнабл>Fкрит то с вероятностью а основная гипотеза о незначимости коэффициента множественной корреляции отвергается, и он признаётся значимым. В этой ситуации включение в модель регрессии всех исследуемых переменных считается обоснованным.
Если Fнабл≤Fкрит , то основная гипотеза о незначимости коэффициента множественной корреляции принимается, и он признаётся незначимым. В этой ситуации построение модели регрессии на основе исследуемых переменных считается необоснованным.
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.
Основная гипотеза состоит в предположении о незначимости коэфф-ов модели множ регрессии, т. е. ![]()
Обратная или конкурирующая гипотеза состоит в предположении о значимости коэффициентов модели множественной регрессии, т. е.![]()
Данные гипотезы проверяются с помощью t-критерия Стьюдента, который вычисляется посредством частного F-критерия Фишера. ![]()
Критическое значение t-критерия определяется как tкрит(а;n-l-1 ), где а – уровень значимости, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров, (n-l-1 ) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.
При проверке основной гипотезы вида
![]()
наблюдаемое значение частного F-критерия Фишера рассчитывается по формуле:
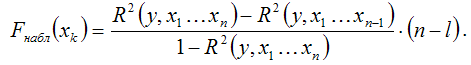
При проверке основной гипотезы возможны следующие ситуации.
Если tнабл≥tкрит , то основная гипотеза о незначимости коэффициента β k модели множественной регрессии отвергается, и он является значимым.
Если tнабл<tкрит , то основная гипотеза о незначимости коэффициента β k модели множественной регрессии принимается.
Поможем написать любую работу на аналогичную тему

