Парная регрессия. - Шпаргалки к экзамену - Эконометрия

Парной регрессией называется уравнение связи двух переменных

у и х  Вида y = f (x),

где у – зависимая переменная (результативный признак);

х – независимая, объясняющая переменная (признак-фактор).

Различают линейные и нелинейные регрессии.

Метод наименьших квадратов МНК

Для оценки параметров регрессий, линейных по этим параметрам, используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических значений ŷx при тех же значениях фактора x минимальна, т. е.

5.   Оценка статистической значимости показателей корреляции, параметров уравнения парной линейной регрессии, уравнения регрессии в целом.

6.   Оценка степени тесноты связи между количественными переменными. Коэффициент ковариации. Показатели корреляции: линейный коэффициент корреляции, индекс корреляции (= теоретическое корреляционное отношение).

Коэффициент ковариации

Мч(у) - Т.е. получим корреляционную зависимость.

Наличие корреляционной зависимости не может ответить на вопрос о причине связи. Корреляция устанавливает лишь меру этой связи, т.е. меру согласованного варьирования.

Меру взаимосвязи  му 2 мя переменными можно найти с помощью ковариации.

, ,

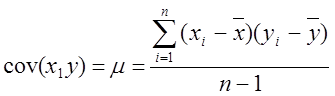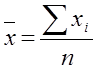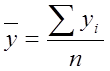
Величина показателя ковариации зависит от единиц в γ измеряется переменная. Поэтому для оценки степени согласованного варьирования используют коэффициент корреляции – безразмерную характеристику имеющую определенный пределы варьирования..

7. Коэффициент детерминации. Стандартная ошибка уравнения регрессии.

Коэффициент детерминации (rxy2) – характеризует долю дисперсии результативного признака y, объясняемую дисперсией, в общей дисперсии результативного признака. Чем ближе rxy2 к 1, тем качественнее регрессионная модель, то есть исходная модель хорошо аппроксимирует исходные данные.

8. Оценка стат значимости показателей корр-ии, параметров уравнения парной линейной регрессии, уравнения регрессии в целом: t-критерий Стьюдента, F-критерий Фишера.

9. Нелинейные модели регрессии и их линеаризация.

Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно исключенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.

Примеры регрессий, нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам:

Нелинейные модели регрессии и их линеаризация

        При нелинейной зависимости признаков, приводимой к линейному виду, параметры множественной регрессии также определяются по МНК с той лишь разницей, что он используется не к исходной информации, а к преобразованным данным. Так, рассматривая степенную функцию

,

мы преобразовываем ее в линейный вид:

,

где переменные выражены в логарифмах.

        Далее обработка МНК та же: строится система нормальных уравнений и определяются неизвестные параметры. Потенцируя значение , находим параметр a и соответственно общий вид уравнения степенной функции.

        Вообще говоря, нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Эта оценка определяется, как и в линейной регрессии, МНК. Так, в двухфакторном уравнении нелинейной регрессии

может быть проведена линеаризация, введением в него новых переменных . В результате получается четырехфактороное уравнение линейной регрессии

10.Мультиколлинеарность. Методы устранения мультиколлинеарности.

Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности.

Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК).

Включение в модель мультиколлинеарных факторов нежелательно по следующим причинам:

ü   затрудняется интерпретация параметров множественной регрессии; параметры линейной регрессии теряют экономический смысл;

ü   оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений, что делает модель непригодной для анализа и прогнозирования

Методы устранения мультиколлинеарности

- исключение переменной (ых) из модели;

Однако нужна определенная осмотрительность при применении данного метода. В этой ситуации возможны ошибки спецификации.

- получение дополнительных данных или построение новой выборки;

Иногда для уменьшения мультиколлинеарности достаточно величить объем выборки. Например, при использовании ежегодных данных можно перейти к поквартальным данным. Увеличение количества данных уменьшает дисперсии коэффициентов регрессии и тем самым увеличивает их статистическую значимость. Однако получение новой выборки или расширение старой не всегда возможно или связано с серъезными издержками. Кроме того, такой подход может увеличить

автокорреляцию.

- изменение спецификации модели;

В ряде случаев проблема мультиколлинеарности может быть решена путем изменения спецификации модели: либо меняется форма модели, либо добавляются новые объясняющие переменные, не учтенные в модели.

- использование предварительной информации о некоторых параметрах;

11.Классическая линейная модель множественной регр-ии (КЛММР). Определение параметров ур-я множественной регр-ии методом наим квадратов.