1. В таблице представлены ряды данных по продовольственным ресурсам (производству 
и импорту 
) и личному потреблению картофеля y (млн. тонн) за 9 лет
|
Год |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
|
|
30.8 |
34.3 |
38.3 Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
37.7 |
33.8 |
39.9 |
38.7 |
37 |
31.4 |
|
|
1.1 |
1.2 |
0.4 |
0.2 |
0.1 |
0.1 |
0.1 |
0.2 |
0.33 |
|
y |
15.7 |
16.7 |
17.5 |
18.8 |
18 |
18.3 |
18.5 |
19.1 |
18 |
Рассчитать вариации и попарные ковариации для этих рядов.
2. По данным таблицы построить уравнение регрессии, приняв личное потребление картофеля за зависимую переменную, а производство и импорт - за объясняющие. Рассчитать коэффициенты при объясняющих переменных.
3. Для регрессии, описывающей линейную зависимость потребления картофеля от производства и импорта , определить свободный коэффициент a.
4. Рассчитать значения личного потребления y картофеля, используя полученное в задаче уравнение регрессии.
5. Рассчитать общую, объясненную и необъясненную сумму квадратов отклонений для рассчитанной ранее регрессии для личного потребления y картофеля.
6. Используя полученные в предыдущем пункте TSS и ESS, рассчитать коэффициент детерминации для регрессии по картофелю.
Решение
Определим выборочные средние 
, 
и 
по формуле (1) при числе наблюдений: n=9
млн. т
млн. т
млн. т
Рассчитаем вариации и попарные ковариации для этих рядов. Вариации для рядов объясняющих переменных и можно вычислить по зависимостям (11)
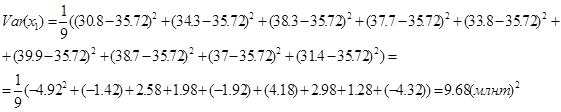
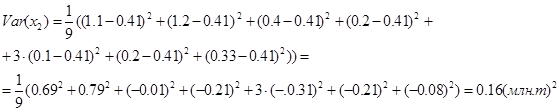
А вариацию зависимой переменной y по зависимости (12)
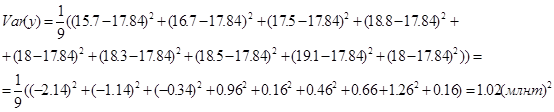
Попарные ковариации для этих рядов определяются по (13) как
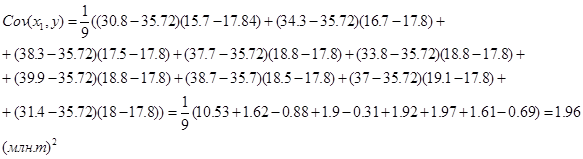
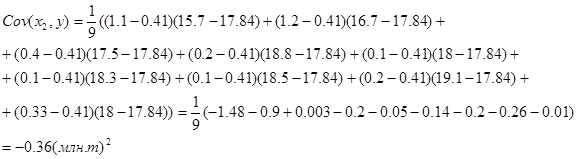
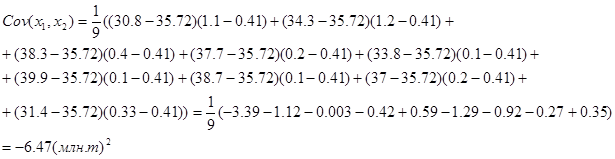
По данным таблицы построим уравнение регрессии
,
Приняв личное потребление фруктов за зависимую переменную, а производство и импорт - за объясняющие, предварительно рассчитав коэффициенты при объясняющих переменных.
Расчет коэффициентов 
и 
производим по зависимостям (15) и (16)
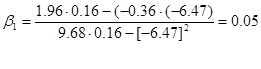
Для регрессии, описывающей линейную зависимость потребления фруктов от производства и импорта , определить свободный коэффициент a.
Свободный коэффициент 
уравнения регрессии вычисляется как
млн. т
Рассчитаем значения личного потребления y фруктов, используя полученное в задаче уравнение регрессии.
Расчет значений 
по зависимости
сведен в табл.2.
Таблица 2
|
Год |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
|
|
16.16 |
16,21 |
18,04 |
18,38 |
18,31 |
18,73 |
18,65 |
18,33 |
17,68 |
|
|
-1,68 |
-1,63 |
0,56 |
0,54 |
0,47 |
0,89 |
0,81 |
0,49 |
-0,16 |
|
( |
2,82 |
2,66 |
0,3 |
0,3 |
0,2 |
0,8 |
0,7 |
0,24 |
0,03 |
|
yi |
15,7 |
16,7 |
17,5 |
18,8 |
18 |
18,3 |
18,5 |
19,1 |
18 |
|
(yi - |
-2,14 |
-1,14 |
-0,34 |
0,96 |
0,16 |
0,46 |
0,67 |
1,26 |
0,16 |
|
(yi - |
4,58 |
1,3 |
0,12 |
0,92 |
0,03 |
0,21 |
0,45 |
1,59 |
0,03 |
Рассчитаем общую и объясненную сумму квадратов отклонений для рассчитанной ранее регрессии для личного потребления y фруктов.
Определим объясненную сумму квадратов отклонений ESS по формуле (8)
с помощью результатов, приведенных в табл.2. Тогда получим
Общая сумма квадратов отклонений ТSS находится по зависимости (9)
с использованием данных табл.2. Суммируя результаты, приведенные в последней строке этой таблицы, получим
Используя полученные в предыдущем пункте величины TSS и ESS, рассчитаем коэффициент детерминации 
для регрессии по фруктам в соответствии с (7) как отношение ESS к TSS
Оценим теперь коэффициент корреляции для фактических y и прогнозных значений 
. Фактически, коэффициент детерминации равен квадрату выборочной корреляции между y и , т.е.
В соответствии с зависимостью (20) имеем
,
Вывод: Полученная величина коэффициента корреляции лежит в диапазоне 0,7-0,9, что указывает на хорошее состояние соответствия уравнения регрессии фактическому изменению величины у.
Поможем написать любую работу на аналогичную тему