Методика построения двухфакторной линейной модели.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

1.               метод исключения;

2.               метод включения;

3.               шаговый регрессионный анализ.

Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты — отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).

Простейший из этих методов - исключение из модели фактора (или факторов), в наибольшей степени ответственных за мультиколлинеарность при условии, что качество модели при этом пострадает несущественно (а именно,  снизится несущественно).

Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции.

К примеру, в линейной множественной регрессии:

параметры при x называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Выбор форм связи затрудняется тем, что, используя математический аппарат, теоретически зависимость между признаками может быть выражена большим числом различных функций.

Наиболее приемлемым способом определения вида исходного уравнения регрессии является метод перебора различных уравнений.  Существует пять основных типов моделей:

- Линейная:

- Степенная  

- Показательная

- Параболическая

- Гиперболическая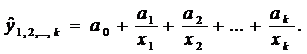

Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации.  Нелинейные формы зависимости приводятся к линейным путем линеаризации. 

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии.

Так, для линейной функции система нормальных уравнений составит:

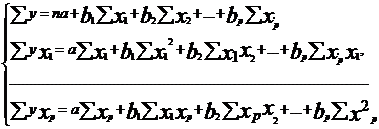
Для ее решения может быть применен метод определителей:

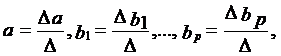
где Δ   —  определитель системы;

      Δа, Δb1,..., Δbp   —  частные определители.

Возможен и иной подход к определению параметров множественной регрессии, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:

,

где 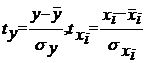- стандартизированные переменные, для которых среднее значение равно 0; ty=tx=0, а среднее квадратическое отклонение sty=stx=1;  βi-стандартизированные коэффициенты регрессии.

К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (β-коэффициенты) определяются из следующей системы уравнений:

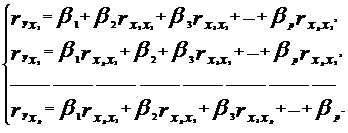Связь коэффициентов множественной регрессии bi со стандартизированными коэффициентами βi описывается соотношением:

Параметр  определяется как  .