Дисперсия - среднее арифметическое из квадратов отклонений наблюденных значений (x1, x2,...,xn) случайной величины от их среднего арифметического. Гомоскедастичность остатков означает, что для каждого значения фактора xj остатки 
имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетеродастичности можно наглядно видеть из поля корреляции.
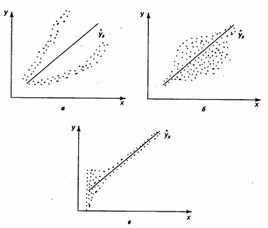
а — дисперсия остатков растет по мере увеличения х;
б — дисперсия остатков достигает максимальной величины при средних значениях переменной х и уменьшается при минимальных и максимальных значениях х;
в — максимальная дисперсия остатков при малых значениях х и дисперсия остатков однородна по мере увеличения значений х.
Наличие гомоскедастичности или гетероскедастичности можно видеть и по графику зависимости остатков 
от теоретических значений результативного признака 
.
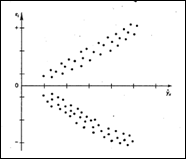Большая дисперсия 
для больших значений 
.
Гетероскедастичность будет сказываться на уменьшении эффективности оценок 
В частности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии 
предполагающей единую дисперсию остатков для любых значений фактора. Практически при нарушении гомоскедастичности мы имеем неравенства:
или 
При этом величина 
может меняться при переходе от одного значения фактора 
к другому. Это означает, что сумма квадратов отклонений для зависимости 
при наличии гетероскедастичности должна иметь вид: 
При минимизации этой суммы квадратов отдельные ее слагаемые взвешиваются: наблюдениям с наибольшей дисперсией придается пропорционально меньший вес.
Задача состоит в том, чтобы определить величину 
и внести поправку в исходные переменные. С этой целью рекомендуется использовать обобщенный метод наименьших квадратов, который эквивалентен обыкновенному МНК, примененному к преобразованным данным. Чтобы убедиться в необходимости использования обобщенного МНК, обычно не ограничиваются визуальной проверкой гетероскедастичности, а приводят ее эмпирическое подтверждение.
При малом объеме выборки для оценки нарушения гомоскедастичности можно использовать метод Гольдфельда-Квандта, который включает:
1.Упорядочение наблюдений n по мере возрастания переменной х.
2. Исключения из рассмотрения центральных наблюдений C; при этом 
где p – число оцениваемых параметров.
3. Разделение совокупности 
на две группы (с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии.
4. Определение остаточной суммы квадратов для обеих групп 
и 
и нахождение их отношения: 
При выполнении нулевой гипотезы о гомоскедастичности отношение R будет соответствовать F-критерию с 
степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табл. значение F-критерия, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин.
Поможем написать любую работу на аналогичную тему