Гетероскедастичность. Линейная модель множе регрессии при гетероскедастичности остатков.

Гетероскедастичность — понятие, используемое в прикладной статистике (чаще всего — вэконометрике), означающее неоднородность наблюдений, выражающуюся в неодинаковой (непостоянной) дисперсии случайной ошибки регрессионной (эконометрической) модели. Гетероскедастичность противоположна гомоскедастичности, означающей однородность наблюдений, то есть постоянство дисперсии случайных ошибок модели.

Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с помощью метода наименьших квадратов. Кроме того, в этом случае оказывается смещённой и несостоятельной классическая оценка ковариационной матрицы МНК-оценок параметров. Следовательно статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим тестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей.

В случае линейной регрессионной моделью с гетероскедастичными остатками ковариационная матрица имеет вид:

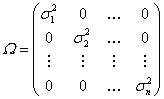                                           (2.2)

 Для оценки параметров модели Y = Xb + e (e  – случайный вектор; X — неслучайная (детерминированная) матрица;) можно применить обычный метод наименьших квадратов. Однако, можно показать, что оценка, полученная с помощью обычного МНК, хотя и будет состоятельной, но не будетоптимальной в смысле теоремы Гаусса–Маркова. Для получения наиболее эффективной оценки нужно использовать другую оценку, получаемую так называемым обобщенным методом наименьших квадратов, рассмотренным ниже.

Укажем, что на практике нередки ситуации, когда прослеживается механизм влияния результатов предыдущих наблюдений на результаты последующих. Математически это выражается в том, что случайные величины ei в регрессионной модели не оказываются независимыми, в частности, условие  не  выполняется.

Способы снижения гетероскедастичности

1.                  Использование взвешенного метода наименьших квадратов (ВМНК, WLS). В этом методе каждое наблюдение взвешивается обратно пропорционально предполагаемому стандартному отклонению случайной ошибки в этом наблюдении. Такой подход позволяет сделать случайные ошибки модели гомоскедастичными. В частности, если предполагается, что стандартное отклонение ошибок пропорционально некоторой переменной Z, то данные делятся на эту переменную, включая константу.

2.                  Замена исходных данных их производными, например, логарифмом, относительным изменением или другой нелинейной функцией. Этот подход часто используется в случае увеличения дисперсии ошибки с ростом значения независимой переменной и приводит к стабилизации дисперсии в более широком диапазоне входных данных.

3.                  Определение «областей компетенции» моделей, внутри которых дисперсия ошибки сравнительно стабильна, и использование комбинации моделей. Таким образом, каждая модель работает только в области своей компетенции, и дисперсия ошибки не превышает заданное граничное значение. Этот подход распространен в области распознавания образов, где часто используются сложные нелинейные модели и эвристики.