Сущность всех методов исключения тенденции заключается в том, чтобы устранить воздействие фактора времени на формирование уравнений временного ряда. Основные методы делят на 2 группы:
- основанные на преобразовании уровней ряда в новые переменные, не содержащие тенденции. Полученные переменные используем далее для анализа взаимосвязи изучаемых временных рядов. Эти методы предполагают устранение трендовой компоненты Т из каждого уровня временного ряда. 1.Метод последовательных разностей. 2.Метод отклонения от трендов.
- основанные на изучении взаимосвязей исходных уровней временных рядов при исключении воздействия фактора времени на зависимую и независимые переменные модели: включение в модель регрессии фактора времени.
Метод отклонений от тренда
Пусть имеются два временных ряда 
и 
, каждый из которых содержит трендовую компоненту Т и случайную компоненту 
.
Проведение аналитического выравнивания по каждому из этих рядов позволяет найти параметры соответствующих уравнений трендов и определить расчетные по тренду уровни 
и 
соответственно. Эти расчетные значения можно принять за оценку трендовой компоненты Т
каждого ряда. Поэтому влияние тенденции можно устранить путем вычитания расчетных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. Дальнейший анализ взаимосвязи рядов проводят с использованием не исходных уровней, а отклонений от тренда 
и 
при условии, что последние не содержат тенденции.
Метод последовательных разностей
В ряде случаев вместо аналитического выравнивания временного ряда с целью устранения тенденции можно применить более простой метод — метод последовательных разностей.
Если временной ряд содержит ярко выраженную линейную тенденцию, ее можно устранить путем замены исходных уровней ряда цепными абсолютными приростами – первыми последовательными разностями.
Пусть
где 
- случайная ошибка.
Тогда 
Коэффициент b — константа, которая не зависит от времени. При наличии сильной линейной тенденции остатки 
достаточно малы и в соответствии с предпосылками МНК носят случайный характер. Поэтому первые разности уровней ряда 
не зависят от переменной времени, их можно использовать для дальнейшего анализа.
Если временной ряд содержит тенденцию в форме параболы второго порядка, то для ее устранения можно заменить исходные уровни ряда на вторые разности.
Пусть имеет место соотношение 
Тогда:
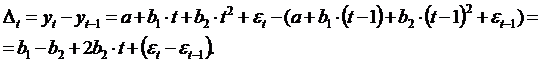
Как показывает это соотношение, первые разности 
непосредственно зависят от фактора времени t и, следовательно, содержат тенденцию.
Определим вторые разности:
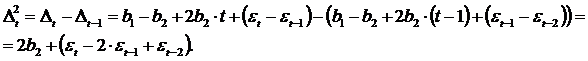
Очевидно, что вторые разности 
не содержат тенденции, поэтому при наличии в исходных уровнях тренда в форме параболы второго порядка их можно использовать для дальнейшего анализа. Если тенденции временного ряда соответствует экспоненциальный или степенной тренд, метод последовательных разностей следует применять не к исходным уровням ряда, а к их логарифмам.
Включение в модель регрессии фактора времени
В корреляционно-регрессионном анализе устранить воздействие какого-либо фактора можно, если зафиксировать воздействие этого фактора на результат и другие включенные в модель факторы. Этот прием используется в анализе временных рядов, когда тенденция фиксируется через включение фактора времени в модель в качестве независимой переменной.
Модель вида 
, относится к группе моделей, включающих фактор времени. Очевидно, что число независимых переменных в такой модели может быть больше единицы. Кроме того, это могут быть не только текущие, но и лаговые значения независимой переменной, а также лаговые значения результативной переменной.
Преимущество данной модели по сравнению с методами отклонений от трендов и последовательных разностей в том, что она позволяет учесть всю информацию, содержащуюся в исходных данных, т.к 
и 
есть уровни исходных временных рядов. Кроме того, модель строится по всей совокупности данных за рассматриваемый период в отличие от метода последовательных разностей, который приводит к потере числа наблюдений. Параметры a и b модели с включением фактора времени определяются обычным МНК.
Поможем написать любую работу на аналогичную тему