Обработка результатов совокупных и совместных измерений

Эти виды измерений характеризуются тем, что значения искомых величин Q1, Q2, Q3,¼  рассчитывают по системе уравнений, связывающих их с некоторыми другими величинами Xi, Yi, Zi,¼,li, i =1,¼, n, измеряемыми прямыми или косвенными методами. Совместные и совокупные измерения обычно выполняют так, чтобы получаемое число уравнений, связывающих искомые величины, превышает число последних. При этом из-за погрешностей измерений даже при точной известной зависимости между величинами нельзя найти такие значения неизвестных, при которых все уравнения выполнялись бы. В этих условиях значения неизвестных, принимаемых за их оценки, находят с помощью метода наименьших квадратов.

В общем виде получаем систему уравнений вида .     

Если являются значениями одной и той же величины, то измерения совокупные; если же - значения разных физических величин, то мы имеем дело с совместными измерениями.

Как уже отмечалось, обычно число уравнений системы (1.79) превышает число неизвестных и из-за погрешностей измерений нельзя найти такие оценки искомых величин, чтобы удовлетворились все уравнения. Поэтому уравнения (1.79) в отличие от обычных математических уравнений принято называть условными. При подстановке в условные уравнения (1.79) найденных каким-то путём значений неизвестных по отмеченным выше причинам получим .

Величины vi принято называть невязкими. Всеобщее признание получил метод решения условных уравнений, который приводит к минимуму сумму квадратов невязок, - метод наименьших квадратов. Теоретически показано, что при нормальном распределении погрешностей метод наименьших квадратов приводит к оценкам неизвестных, удовлетворяющих принципу максимума правдоподобия, т.е. наиболее вероятным оценкам.

Мы остановимся на практическом применении метода наименьших квадратов. Рассмотрим применение метода для измерений, при которых уравнения являются линейными. Для сокращения записей возьмём случай с тремя неизвестными.

Пусть система условных уравнений имеет вид    i=1,¼,n;  n>3 ,             причем Q1, Q2, Q3   - искомые неизвестные; Xi, Yi, Zi, li   - результаты i-го наблюдения и известные коэффициенты.

В общем случае число неизвестных Qj равно m (j=1,¼,m), причем m<n; если m=n, то система условных уравнений решается однозначно, хотя получающиеся результаты и отягощены погрешностями.

Если подставить какие-то оценки искомых величин , то получим невязки  

Найдем оценки , , из условия .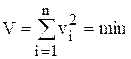                                   

Для выполнения этого условия необходимо, чтобы .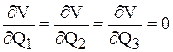                                          

Найдем эти частные производные и приравняем их к нулю: ,,.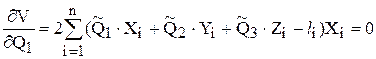                     

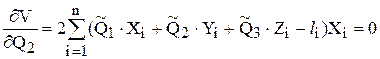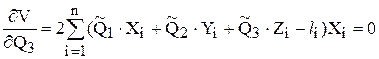Отсюда получаем систему так называемых нормальных уравнений:,, .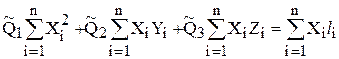         

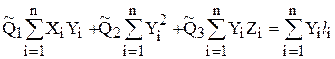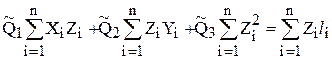При написании нормальных уравнений часто пользуются обозначениями: 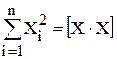,  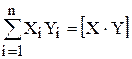  и т.д. Очевидно, что 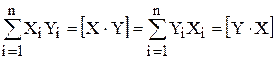,  т.е. =.

Тогда уравнения принимают более простой вид:

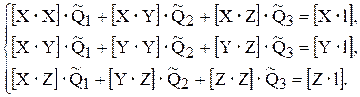
Нужно обратить внимание на две хотя и очевидные, но важные особенности матрицы коэффициентов при неизвестных в системе:

            1 Матрица этих коэффициентов симметрична относительно главной диагонали.

            2 Все элементы главной диагонали положительны.

Эти свойства являются общими, они не зависят от числа неизвестных, но в данном примере показаны применительно к случаю с тремя неизвестными.

Число нормальных уравнений равно числу неизвестных, и их решение известными методами дает интересующие нас оценки искомых величин. Наиболее кратко решение записывается с помощью определителей: , , 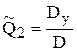 ,      где .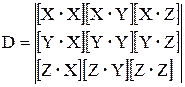    

Определитель Dx получают из главного определителя системы D путем замены столбца с коэффициентами при неизвестном  на столбец со свободными членами:  .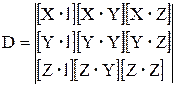                                              

Определители DY и DZ находят аналогично, т.е. путем замены на указанный столбец второго и соответственно третьего столбца.

Теперь нужно оценить погрешности полученных результатов. Задача решается в том случае, когда из числа непосредственно измеряемых величин можно выделить одну, погрешность измерения которой существенно превышает погрешности измерений остальных. Условные уравнения тогда преобразуются так, чтобы, величина, измеряемая с наибольшей погрешностью, была выделена в свободный член li. В этом случае оценки с.к.о. найденных значений неизвестных можно вычислить, пользуясь формулами: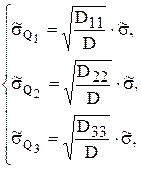            

где    D11, D22, D33  -  алгебраические дополнения элементов , и определителя D соответственно (они получаются путем удаления из матрицы определителя D столбца и строки, на пересечении которых находится данный элемент);        - с.к.о. условных уравнений.

Оценка с.к.о. условных уравнений вычисляется по формуле 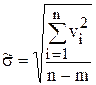, где vi - невязка условного уравнения, полученная  при  подстановке в него оценок  , , .

Доверительные границы случайной погрешности измерения искомых величин определяют на основе распределения Стьюдента, при этом число степеней свободы n-m:  ,        где tp  - коэффициент Стьюдента, находящийся исходя из значений числа степеней свободы n-m и доверительной вероятности Р.