Истечение жидкости через отверстия в тонкой стенке при постоянном уровне - ГИДРАВЛИКА  И ГИДРОПРИВОД. КОНСПЕКТ ЛЕКЦИИ

Выведем формулы скорости и расхода жидкости при истечении через малое отверстие. Пусть жидкость вытекает из большого резервуара через малое отверстие в его дне или стенке (рис. 39).

Опытами установлено, что сжатое сечение струи находится от внутренней поверхности резервуара на расстоянии около половины диаметра отверстия. Эта величина обычно бывает мала сравнительно с напором Н в резервуаре, и можно считать, что центр отверстия и центр сжатого сечения струи находятся на одинаковой высоте, тем более при отверстии в боковой стенке.

Высоту уровня жидкости в резервуаре Н над центром отверстия называют геометрическим напором. В общем случае давление  в резервуаре отличается от давления  в пространстве, куда истекает жидкость.

Проведем плоскость сравнения 2-2 через центр сжатого сечения струи.

Уравнение Д. Бернулли применить к сечению отверстия нельзя, так как струйки в последнем сходятся под большими углами, и движение жидкости в нем не плавно изменяющееся.

Напишем уравнение Д. Бернулли для сечений 1-1 и 2-2

,                 (124)

где – скорость подхода жидкости к отверстию в резервуаре; – средняя скорость течения в сжатом сечении; – коэффициент местного сопротивления при истечении через отверстие.

Перенесем наружное давление  в левую часть и обозначим величину

.                                      (125)

Эта величина называется напором истечения.

В правой части уравнения (124) вынесем за скобки . Тогда уравнение Д. Бернулли сведется к

,

откуда

.

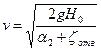Обозначим величину

.                                                    (126)

Величину  называют коэффициентом скорости.

С учетом введенного обозначения

.                                           (127)

Так как коэффициент Кориолиса , а коэффициент местных потерь напора в отверстии , то . По опытным данным , а . Отсюда

.

Для идеальной жидкости  и . Тогда

.                                            (128)

Это уравнение называется формулой Торичелли. Оно показывает, что скорость в начале вытекающей струи равна скорости свободного падения тела, упавшего с высоты .

Когда поперечное сечение резервуара много больше площади живого сечения отверстия, а скорость жидкости в резервуаре незначительна (к примеру, меньше 0,1 м/сек), то скоростным напором  можно пренебречь. В случае, когда давления снаружи и в резервуаре одинаковы , то весь напор истечения сводится к геометрическому напору, т. е. . Это бывает обычно при расчете истечения из открытых резервуаров в атмосферу.

Расход жидкости определится как произведение скорости истечения на площадь сжатого сечения струи

,                         (129)

где – коэффициент сжатия струи, равный отношению площади сжатого сечения  к площади отверстия .

Величину  обозначают через  и называют коэффициентом расхода.

Таким образом, расход жидкости, вытекающей через отверстие, определяют по формуле

.                                        (130)

При точных измерениях размеров сжатого сечения струи установлено, что при совершенном сжатии струи . В этом случае . В общем же случае коэффициент расхода  зависит от условий сжатия.

При истечении не в газовую среду, а в смежный резервуар с той же жидкостью (что принято называть истечением «под уровень»), т. е. когда отверстие затоплено с обеих сторон, в качестве геометрического напора Н принимают разность уровней жидкости в резервуарах. Числовые значения коэффициентов ,  и  остаются при этом практически теми же.

В случае круглого отверстия, расположенного на значительном расстоянии от стенок, струя сжимается со всех сторон одинаково, и в сжатом сечении имеет также форму круга; при этом сжатое сечение находится от кромок отверстия на расстоянии около половины диаметра отверстия – . Величина коэффициента сжатия зависит от относительных размеров отверстия и от положения его относительно стенок резервуара и поверхности жидкости.

В зависимости от расположения отверстия различают следующие виды сжатия (рис. 40):

1) полное сжатие со всех сторон (отверстия 1 и 2);

2)   неполное,   когда   сжатия   нет   с   одной   или нескольких сторон (отверстия 3, 4 и 5).

Полное сжатие подразделяют на:

а)    совершенное, когда  и  (отверстие 1);

б)    несовершенное, когда  и  (отверстие 2).

Форма   сечения   струи   жидкости   при истечении претерпевает изменения.

Эти изменения называются инверсией. Инверсия происходит вследствие того, что скорости подхода к отверстию в разных точках его периметра различны и вследствие сил поверхностного натяжения. На рис. 41 показано изменение формы струи при истечении через квадратное отверстие по мере удаления от резервуара.

При    несовершенном    сжатии    коэффициент расхода  вычисляют по формулам:

для круглых отверстий

                     (131)

для прямоугольных отверстий

                    (132)

где – значение коэффициента расхода при совершенном сжатии;  и – поправочные коэффициенты, зависящие от отношения площади сечения отверстий  к площади сечения сосуда . Значения этих коэффициентов принимают по таблице:

Значение величин  и  при несовершенном сжатии

При неполном сжатии коэффициент расхода вычисляют по уравнениям:

для круглых отверстий

;                                   (133)

для прямоугольных отверстий

,                             (134)

где – коэффициент расхода при полном сжатии; – часть периметра, на котором нет сжатия; Р – полный периметр отверстия.

При   расчете   больших   отверстий   значения   коэффициентов  расхода, рекомендованных Н. Н. Павловским, приведены в таблице:

Значения коэффициентов расхода для больших отверстий