Итак, в классическом нашем обычном макромире хаос в нелинейных системах играет доминирующую роль. В таком случае, если учесть ещё, что квантовая физика изначально вероятностна, то в микромире его проявление должно быть в значительно большей мере. Известен принцип соответствия Бора, согласно которому классическая физика – частный, предельный, случай проявления квантовых эффектов, когда размер системы превышает атомный.
Оказывается (теорема Колмогорова–Арнольда–Мазера) структуры правильной формы при малых возмущениях выживают. По этой теореме можно определять возмущения, вызывающие хаотическое поведение регулярных систем. Например, движение электрона в атоме водорода иногда приобретает хаотичность. Без внешнего воздействия разрешенные значения энергий электрона в атоме при подводе ее извне все больше приближаются друг к другу, то есть растет размер атома и атом становится классической системой, в которой выполняются законы Ньютона.
В сильном магнитном поле атом ведет себя хаотично. В этом случае ось симметрии ориентирована вдоль направления поля и электрон движется в двухмерной плоскости. Поэтому нет движения вокруг оси, но есть оно вдоль и поперек нее. Здесь можно, по Пуанкаре, использовать двухмерную плоскость и следить за точками, в которых траектория пересекает эту плоскость. Хаос в микромире проявляется в распределении уровней электронов атомов (их орбит) и влияет на волновую природу квантового мира.
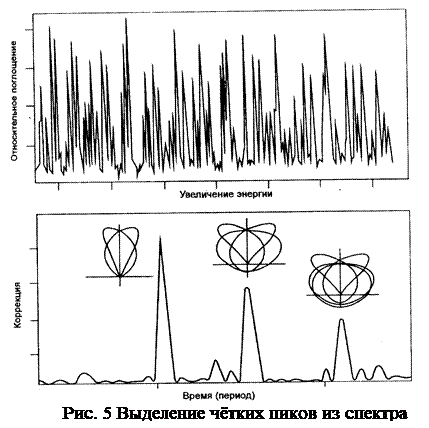
При возбуждении атома (при переходе электронов на далекие от ядра уровни, или орбиты) уровни энергии атома кажутся неупорядоченными. Фурье-анализ позволяет выделить из спектра ряд отчетливых пиков, точно соответствующих классическим (боровским) периодическим орбитам электронов. Особенно интересна связь квантового хаоса и теории чисел. Например, значения чисел, обращающих дзета-функцию Римана в нуль, напоминают энергетический спектр атома (рис. 5). Почему так – неясно!
Итак, идея молекулярного беспорядка ликвидировала различия в механистическом и статистическом описаниях. Идеи беспорядка появились и в классических науках, теории поля Максвелла и в гипотезе Планка, в небесной механике. Особенно развились они в квантовой теории. Далее установили, что случайные воздействия могут влиять и на динамические системы, доводя их до хаоса – это нелинейные колебательные системы. Их эволюцию прослеживают по фазовым траекториям. В них появляются аттракторы, отражающие стремление системы к равновесию. Область хаотических траекторий – странный аттрактор - обнаруживает фрактальность, присущую многим явлениям.
Пороговый характер самоорганизации отражен в понятии катастрофы, скачкообразном изменении параметров системы, вызванном плавными внешними воздействиями. Теория катастроф свела множества сложных случаев к небольшому набору уже исследованных схем. Она применима во всех областях знаний без исключения для систем, далеких от равновесия. Странные аттракторы обнаружили, по Фейгенбауму, законы перехода к хаосу, когда период, о котором говорилось (рис. 4 и 5), удваивается. Наличие законов перехода, когда точка бифуркации, в которой параметр меняется скачкообразно, позволяет назвать хаос детерминированным.
По теории самоорганизованной критичности каждая часть большой системы переходит к своему критическому состоянию, в котором малые изменения параметров могут вызвать цепную реакцию. Оказалось, например, что земная кора находится в критическом состоянии (состояние «слабого хаоса», где возможны еще прогнозы). Это же можно сказать и о слабо возбужденных атомах (смотрите рис. 5). А вот при сильном возбуждении атомы (точнее электроны в них!) обнаруживают хаотическое поведение и, согласно принципу соответствия Бора, квантовая механика переходит в классическую, применяемую в предельном случае объектов с размерами больше атомных.
Поможем написать любую работу на аналогичную тему