Относительное равновесие жидкости

Относительным равновесием жидкости называется такое состояние, при котором каждая ее частица сохраняет свое положение относительно твердой стенки движущегося сосуда. При относительном равновесии рассматриваются две задачи: характер распределения давления и форма поверхности уровня (равного давления). Решаем эти задачи опять же используя полученное нами на прошлой лекции уравнение для определения гидростатического давления

При   р=const  Xdx+Ydy+Zdz=0                                                                (3.4)

         В общем случае любое сложное движение сосуда с жидкостью можно представить в виде суммы трех движений: поступательного по вертикали и горизонтали и вращательного.

         1) Движение по вертикали с постоянным ускорением а.

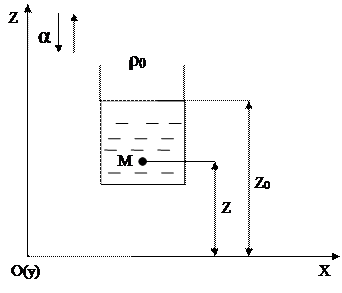         Проекции массовых сил на координатные оси будут: X=0, Y=0, Z=. Знак «-» соответствует равноускоренному подъему резервуара, «+»- спуску.

Характер распределения давления получим следующий

                   ,

Или проинтегрировав

                   +С,

где С- постоянная интегрирования, определяемая из граничных условий на свободной поверхности Z=Z0 и P=P0/

Тогда

         Составим уравнение поверхности уровня

                   (

Если gа, то dz=0, z=const, т.е. поверхности равного давления представляют собой горизонтальные плоскости.

2) Горизонтальное перемещение резервуара с жидкостью с постоянным ускорением а.

В этом случае X=-a, Y=0, Z=-g.

         Закон распределения давления получим

         .

         После интегрирования с учетом граничных условий X=X0, Z=Z0, P=P0 получим закон распределения давления в следующем виде

         .

Т.о. распределение давления в жидкости подчиняется основному закону гидростатики для любой фиксированной вертикали.

         Поверхность равного давления определится уравнением

         После интегрирования

Или

Т.о. поверхностями равного давления будут плоскости, углы наклона которых к горизонтальной плоскости определяются угловым коэффициентом, равным –a/g. 

         3) Вращение цилиндрического сосуда с жидкостью с постоянной угловой скоростью        .

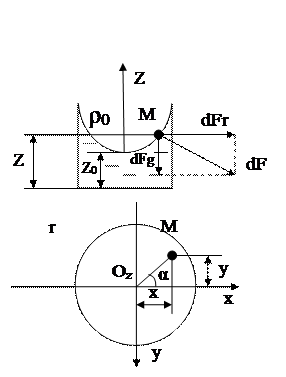
         В этом случае проекции массовых сил: X= , Z= -g.

         Поверхность равного давления определяется уравнением

         Или проинтегрировав

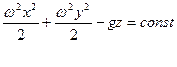
Или учитывая, что  получим

                   .

Откуда

         Т.о. при вращении сосуда с жидкостью вокруг вертикальной оси поверхностями равного давления будет семейство параболоидов вращения, осью которых является ось Oz.

         Закон распределения давления получим

Или

         После интегрирования с учетом граничных условий r =0, z=z0, p=p0 получим закон распределения давления:

                   .

         Это уравнение показывает, что распределение давления подчиняется линейному закону для любой фиксированной круглоцилиндрической поверхности.