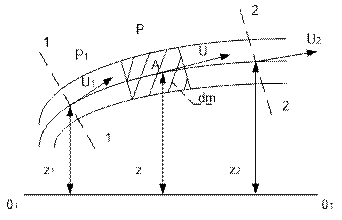
Для вывода уравнения Бернулли применительно к элементарной струйки вязкой жидкости рассмотрим его энергетический смысл. С этой целью подсчитаем механическую энергию бесконечно малой частицы массой dm с центром в т. А, находящейся в пределах элементарной струйки, относительно горизонтальной плоскости сравнения О1 – О1 (рис. 5.1)
Как известно, потенциальная энергия равна:
Кинетическая энергия:
Полная механическая энергия состоит из суммы кинетической и потенциальной энергий:
Отнесем энергию к единице веса жидкости, т.е. определим удельную энергию
Таким образом, получим выражение, которое является уравнением Бернулли и выражает закон сохранения энергии: вдоль элементарной струйки идеальной жидкости сумма потенциальной и кинетической энергии постоянная величина, т.е.
Сумма 
представляет собой потенциальную энергию, состоящую из удельной энергии положения z и удельной энергии давления 
. Выражение 
называется удельной кинетической энергией.
Вдоль элементарной струйки удельные кинетическая и потенциальная энергии могут изменяться, но их сумма остается постоянной.
При движении вязкой жидкости суммарная удельная энергия движущейся жидкости вдоль струйки убывает в силу различных гидравлических сопротивлений. Следовательно, для элементарной струйки вязкой жидкости, находящейся в установившемся движении:
Чтобы получить равенство левой и правой части, необходимо в правой части добавить дополнительный член hΣ, обозначающий затрату удельной энергии на преодоление сопротивлений при движении реальной вязкой жидкости в пределах между первым и вторым сечениями. В этом случае уравнение Бернулли принимает вид:
Затрачиваемая на преодоление гидравлических сопротивлений часть энергии превращается из механической в тепловую, причем необратимо. В связи с этим можно считать
потерянной удельной энергией.
Поможем написать любую работу на аналогичную тему