Уравнение Бернулли для элементарной струйки идеальной жидкости. - Лекции по гидравлике и гидроприводу

Вспомним уравнение Эйлера для элементарной струйки идеальной жидкости:

Приведем систему уравнений к виду удобному для интегрирования, для чего умножим каждое из уравнений на dx, dy, dz и почленно сложим:

            Первый трехчлен уравнения  является полным дифференциалом гидродинамического давления, отнесенным к единице плотности и равен:  

            Рассмотрим движение жидкости только под действием силы тяжести, тогда внешние массовые силы, заданные в виде проекций ускорений на соответствующие координатные оси, будут X=0, Y=0, Z=-g. Тогда второй трехчлен будет равным – gdz.

Первую часть уравнения  преобразуем зная, что перемещения соответственно равны:    dx = Uxdt, dy = Uydt, dz = Uzdt.

Тогда: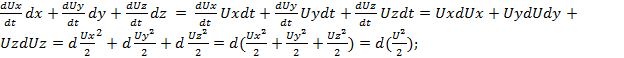

где U – местная скорость в сечении струйки.

            Подставляя в уравнение  полученные значения, запишем:

  или                 

Если разделить уравнение  на g, получим уравнение, отнесенное к единице веса:

Поле интегрирования получим:

Выражение  было получено в 1738 г. академиком Российской Академии наук Д. Бернулли и названо уравнением Бернулли для элементарной струйки идеальной жидкости.