КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

Задача кинематики - описание движения среды независимо от внешних условий, которые инициируют и поддерживают движение. Т.к. СС представляет собой непрерывную совокупность точек, то чтобы описать её движение, необходимо описать движение ВСЕХ точек.

Движение обычно определяется по отношению к некоторой системе отсчёта, которую мы называем системой координат. Если нет особой оговорки, то через х1, х2, х3  будем обозначать координаты любой ортогональной системы.

Способ Лагранжа.  Задаются законы  изменения положения (подвижная система отсчёта), скорости, ускорения и других величин, то есть кинематические уравнения движения:

хi = xi (x1,x2,x3, t)  (i = 1,2,3),                                                   (1.1)

где  xi являются координатами фиксированной (индивидуальной) точки среды. Совокупность величин  x и  t называются переменными Лагранжа.

Построение математической модели любой СС опирается на понятие закона движения.

Запишем проекции скоростей и ускорений точек среды на оси координат хi, которые определяются обычными равенствами:

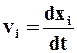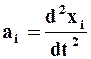,                                                                         (1.2)

Способ Эйлера.  Задаются перемещение, скорость, ускорение в точке пространства (неподвижная система отсчёта), мимо которой в данный момент проходят частицы среды, как функции координат точек пространства xi и времени t:

ui = ui (x1, x2,  x3 , t);

vi = vi (x1, x2,  x3 , t);                                                            (1.3)

ai = ai (x1, x2,  x3 , t).

Совокупность параметров  хi   и  t  называют переменными Эйлера.

Переход от переменных Лагранжа к переменным Эйлера и наоборот. Если у нас есть закон движения СС в форме (1.1), то чтобы перейти к переменным Эйлера необходимо разрешить уравнения (1.1) относительно xi .

xi = xi(x1, x2,  x3 , t).                                                                      (1.4)

При  фиксированных координатах хi эти соотношения указывают те точки xi  СС, которые в разные моменты времени проходят через данную точку пространства.

Для перехода от переменных Лагранжа к переменным Эйлера (хi, t), необходимо в формулы для проекций скоростей vi = vi (x1,x2,x3, t)и других величин подставить соотношения (1.4).

 Пусть задано распределение скорости в форме Эйлера (1.3), тогда, учитывая равенства (1.2) , получим СИСТЕМУ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ относительно хi :

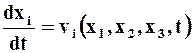 где (i =  1,2,3)

Решая эту систему, определим хi = хi(С1, С2, С3, t), где  - С1, С2, С3 - постоянные, определяемые по хi при t = t0, то есть,  они являются координатами индивидуальной точки сплошной среды (переменными Лагранжа).