При рассмотрении движения жидкостей и газов в пластах, представляющих собой проницаемую среду, необходимо знать характер изменения давления в точках пласта и на его границах, а особенно на стенках скважины, а также расход пластовых флюидов через какие-либо ограничивающие поверхности.
При бурении это представляет интерес с позиций оценки процессов газоводонефтепроявлений, поглощений, проникновения бурового раствора и продуктивные пласты, ухудшения проницаемости призабойной зоны и др.
В самом общем случае уравнение движения в неизменяемой пористой среде для жидкостей и газов, подчиняющихся закону Дарси, в прямоугольной системе координат Оxyz, согласно Л.С. Лейбензону, имеет вид
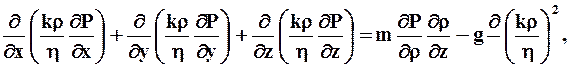
где k - коэффициент проницаемости пористой среды;
P - давление; r =f (P) - плотность жидкости или газа; h - вязкость жидкости или газа; g - ускорение силы тяжести.
В случае, если жидкость несжимаема (r = const), то уравнение движения приобретает следующий вид:
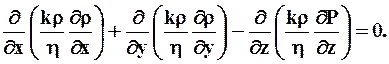
В случае k = f (xyz) без знания вида этой функции для пластов решение уравнений движения невозможно, и это усложняет описание большого числа практических задач.
В предположении k = const и h = const или k / h = const получается простое уравнение Лапласа
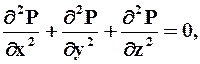
решение которого Р = Р(xyz) в общем случае содержит две постоянные интегрирования и требует задания двух граничных условий.
В этом уравнении давление – лишь функция координат и не зависит от времени, т.е. это случай нестационарной фильтрации.
При течении малосжимаемой жидкости, для которой с достаточной точностью
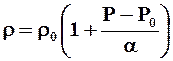 ,
,
где r0 - плотность при Р = Р0; a - модуль объёмной упругости жидкости.
Уравнение движения при k = const и h = const называют уравнением пъезопроводности или упругого режима фильтрации и записывают в виде
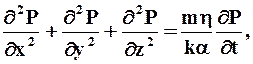
где ka/(mh) = К коэффициент пьезопроводности, по аналогии с коэффициентом температуропроводности в подобном по виду уравнении теплопроводности Фурье, описывающем нестационарное температурное поле.
В случае деформируемости пористой среды уравнение пьезопроводности принимает вид
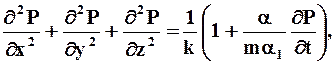
где a1 - модуль, характеризующий упругость пористой среды.
Решение Р = Р(xyz) приведённых уравнений пьезопроводности содержит уже три постоянных интегрирования и требует задания двух граничных и одного начального (при t = 0) условий.
При течении в неизменяемой пористой среде с k = const газа, плотность которого является функцией давления и температуры ; r =f (r, Т) и h = const, уравнения движения записываются в виде
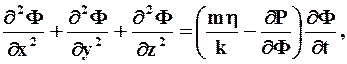
где ![]() - функция Лейбензона.
- функция Лейбензона.
В частном случае политропического процесса
![]() ,
,
где n - показатель политропы; b - коэффициент сверхсжимаемости; RT - газовая постоянная; T - абсолютная температура.
Поможем написать любую работу на аналогичную тему

