УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ

Основным динамическим уравнением движения материальной точки является 2-й закон Ньютона m`a = `F, а широко используемым следствием этого закона являются следующие общие теоремы движения системы материальных точек:

Ø производная по времени от количества движения  равна сумме всех действующих на систему внешних сил 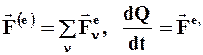 (1.45) и называется уравнением количества движения, или уравнением импульсов:

Ø производная по времени от кинетического момента  системы относительно какого-либо неподвижного центра О равна сумме моментов  всех внешних сил, действующих на систему, относительно того же центра, т.е. 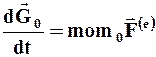 (1.46)  называется уравнением моментов количества движения;

Ø дифференциал кинетической энергии 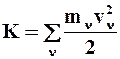 системы равен сумме элементарных работ   всех  действующих на систему внешних   и внутренних   сил, т.е. (1.47) называется уравнением механической энергии или теоремой живых сил.

Для любого мысленно выделяемого индивидуального объёма сплошной среды, ограниченного поверхеностью  , уравнения (1.45-1.47) действительны, если динамические величины определить следующим образом:

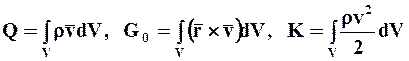
(соответственно количество движения, момент количества движения и кинетическая энергия сплошной среды в объёме V);

(соответственно сумма внешних объёмных и поверхностных сил и их моментов относительно некоторого неподвижного центра О, действующих на среду в объёме V). Силы и их моменты непрерывно определены и сосредоточены.

Сумма элементарных работ внешних и внутренних объёмных и поверхностных сил

.

В этом случае уравнения (1.45) и (1.46) являются основными постулируемыми динамическими соотношениями МСС. Они служат исходными для описания любых движений СС, в том числе разрывных движения и ударных процессов.

Уравнение (1.47) одно из наиболее важных следствий уравнений (1.45) и (1.46) при непрерывных движениях в пространстве и времени.

При непрерывных движениях интегральная теорема движения (1.45) эквивалентна следующим 3 дифференциальным уравнениям:

в декартовой системе координат:

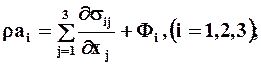
в цилиндрической системе координат при осевой симметрии

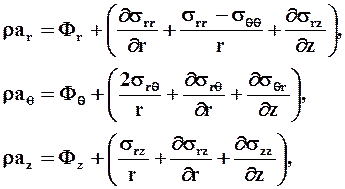
где проекции ускорения   вычисляют по формулам (1.9).

Эти уравнения, связывающие компоненты vi вектора скорости и тензора напряжений   являются основной системой дифференциальных уравнений движения для любой СС, представляющих собой уравнение баланса количества движения (импульса) для бесконечно малого объёма среды.

Если движения частиц происходят без ускорения ( = 0) или они пренебрежимо малы, то уравнения (1.48) называются дифференциальными уравнениями равновесия.

При непрерывном движении сплошной среды теорема моментов количества движения (1.46) в дифференциальной форме сводится к выводу о том, что тензор напряжений симметричен, т.е. s = s  . Если тензор напряжений симметричен, то уравнения моментов количества движения удовлетворяются тождественно.

Интегральная теорема живых сил (1.47) эквивалентна следующему дифференциальному уравнению:

dK = dW = dA(e)  (1.49)

где:

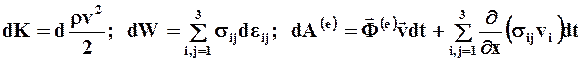
соответственно изменение кинетической и потенциальной энергии бесконечно малого объёма сплошной среды, элементарная работа внешних объёмных и поверхностных сил, действующих на бесконечно малый элемент объёма среды.

Уравнение (1.49) является следствием уравнения движения (1.48) и представляет собой УРАВНЕНИЕ БАЛАНСА МЕХАНИЧЕСКОЙ ЭНЕРГИИ.

В общем случае оно не является законом сохранения энергии, но его можно так трактовать тогда, когда механическая энергия тела не переходит в тепловую или другие виды энергии. Общий закон сохранения энергии в этом случае распадается на два: закон сохранения механической энергии и закон сохранения энергии другого вида.