ПОЛЯ В ГИДРОДИНАМИКЕ

При изучении движения жидкости рассматривают её как сплошную среду. Таким образом, рассматривают не движение конечного числа отдельных частиц, а поля различных физических величин: скорости, плотности, давления и т.д. Такие поля можно назвать материальными полями. Математически эти поля описывают системой функций от координат и времени. Такой подход типичен не только для механики сплошных сред, но и для ряда других областей физики.

В общем случае поле является пространственным (трёхмерным), однако, иногда задачу упрощают, и рассматривают двумерные (плоские) или одномерные поля.  В этом случае полагают, что физические величины зависят от одной или двух пространственных координат.

Если физические величины не зависят от времени, то поле называют стационарным, в противоположном случае - нестационарным.

При математическом описании полей предполагают, что существуют пределы значений физических величин в точке. Такой подход упрощает физическую реальность, так как не учитывает дискретность строения материи, но такая абстракция оправдана, нужно только разумно ограничивать область полученных результатов.

Так как в практических задачах размеры обтекаемых тел намного порядков больше молекулярных размеров, то в этих задачах жидкость можно рассматривать как сплошную среду.

СКАЛЯРНЫМ называют поле, которое характеризуют в каждой точке пространства одним числом. Скалярное поле описывают одной функцией, зависящей от трёх координат. (Например, поле плотности или температуры).

Основное свойство скалярной функции а(х1 ,х2 ,х3) состоит в том, что её численное значение не меняется при преобразовании координат. Если перейти от старой х1 ,х2 ,х3 к новой х¢1 ,х¢2 ,х¢3 системе координат, то значения плотности или температуры в фиксированной  точке пространства, естественно, не изменяются:

а(х¢1 ,х¢2 ,х¢3)= а(х1 ,х2 ,х3).

ВЕКТОРНЫМ называют поле, которое в каждой точке пространства характеризуют ВЕЛИЧИНОЙ и НАПРАВЛЕНИЕМ. Например, поле скоростей жидкости. Вектор а в пространстве трёх измерений может быть задан тремя компонентами:

а1(х1 ,х2 ,х3), а2(х1 ,х2 ,х3), а3(х1 ,х2 ,х3),

то есть, тремя функциями от трёх переменных. Это можно записать в виде матрицы-столбца:

а ÜÞ                    

Введём новую декартову систему координат с тем же началом, НО С ДРУГИМ НАПРАВЛЕНИЕМ ОСЕЙ. Пусть lij  - направляющий косинус оси x¢j относительно оси xi (i = 1,2,3; j = 1,2,3). Вычислим проекции того же вектора на новые оси координат:

a¢1 = l11 a1 + l21 a2 + l31 a3;

a¢2 = l21 a1 + l22 a2 + l23 a3;       

a¢3 = l31 a1 + l32 a2 + l33 a3;

Следовательно, вектор подчиняется определённому закону преобразования его компонент и отличается от скалярной величины, численное значение которой не меняется при преобразовании координат. То есть, сам вектор не меняется в новых координатах, а меняются его компоненты.

Это выражение  можно представить в индексной форме записи в виде суммы:

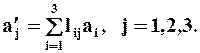
Или ещё более короткой

При такой записи пользуются двумя правилами:

1.      Соглашение о суммировании. По индексу, встречающемуся дважды (немой индекс), производят суммирование от 1 до 3.

2.      Соглашение о ранге. Индекс, встречающийся один раз (свободный индекс), пробегает значения от 1 до 3.

Таким образом, уравнение с одним свободным индексом означает запись трёх уравнений.

Помимо скалярных и векторных полей в МСС рассматриваются ещё и ТЕНЗОРНЫЕ ПОЛЯ.

Рис.1.1 Система напряжений на гранях элементарного объёма (Г.С. Самойлович.  Гидрогазодинамика.С.8).

Вырежем в жидкости элементарный параллелепипед с рёбрами dx1, dx2, dx3 (рис.1.1). На грани этого параллелепипеда со стороны остальной жидкости действуют поверхностные напряжения. В общем случае на каждую грань действуют как НОРМАЛЬНЫЕ так и КАСАТЕЛЬНЫЕ напряжения. В принятой записи каждое из напряжений будет иметь два индекса. Первый индекс означает ориентацию площадки, на которую действует напряжение, второй - ось проектирования.

Компоненты напряжений можно записать в виде матрицы тензора напряжений

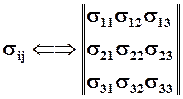 при i = 1,2,3; j = 1,2,3.

Первый индекс означает номер строки, второй - номер столбца. Нормальные напряжения имеют два одинаковых индекса - диагональ матрицы. Касательные напряжения имеют разные индексы.  Ранг тензора равен числу индексов компонент.

Тензор второго ранга описывается в общем случае девятью функциями трёх переменных. Однако этот тензор обладает важной особенностью. Из условия равенства нулю моментов, действующих на элементарный объём следует, что касательные напряжения с одинаковыми, но расположенными в обратном порядке индексами равны: sij = sji. Такой вектор называется симметричным  и может быть записан как:

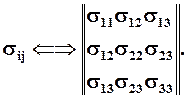
Следовательно, такой тензор напряжений выражается через шесть функций трёх переменных.

Компоненты напряжений представляют как нормальные, так и касательные напряжения. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ВОЗНИКАЮТ ВСЛЕДСТВИЕ ВЯЗКОСТИ, которой обладают все реальные жидкости. В покоящейся вязкой жидкости касательные напряжения отсутствуют, так как скорости деформации равны нулю, а нормальные напряжения вызваны только давлением и не зависят от ориентации площадки. (Закон Паскаля).

Идеальная жидкость это  жидкость, лишённая вязкости. Следовательно, в идеальной жидкости касательные напряжения отсутствуют, и матрица тензора напряжений принимает вид:

.

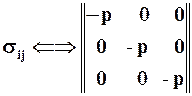Перед Р по условию поставлен знак - минус, так как давление обычно сжимает жидкость, то есть действует против положительного направления нормали к площадке.

Матрицу (1.10) можно сокращённо записать в виде sij  = - P dij,

где dij  = 1 при  i = j; dij = 0 при i ¹ j , СИМВОЛ КРОНЕКЕРА.

Понятие установившегося движения относительно, так как в зависимости от выбранной системы координат одно и то же движение может быть установившимся и неустановившимся.

Пусть распределение плотности задано в переменных Лагранжа:

r = r (x1,x2,x3, t), тогда изменение плотности частицы СС равно  .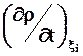

Если функция задана в переменных Эйлера: r = r (x1, x2,  x3, t), необходимо перейти к переменным Лагранжа и воспользоваться правилом дифференцирования сложной функции, в результате чего получим:

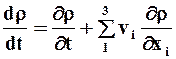
Производная  называется полной производной (индивидуальной, субстанциональной) и характеризует изменение плотности данной частицы сплошной среды в единицу времени.

Производная  называется частной (местной, локальной) и характеризует изменение плотности в данной точке пространства в единицу времени.

Величина 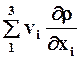 называется конвективной производной.

Аналогично формуле (1.5) можно написать формулы для определения полной производной по времени проекций любой векторной величины, заданной в переменных Эйлера.

Для любого векторного поля используют понятие векторных линий. Векторные линии - это семейство линий, касательные к которым совпадают с направлением вектора. В случае поля скоростей эти линии принято называть ЛИНИЯМИ ТОКА.

Если выбрать произвольную кривую  С, не совпадающую с линией тока, и через каждую её точку провести линию тока, то образуется ПОВЕРХНОСТЬ ТОКА. Если кривая  С замкнута, поверхность тока превращается в ТРУБКУ ТОКА.

Аналитически семейство линий тока можно найти из условия коллинеарности (расположения на одной прямой или на параллельных) элемента , взятого вдоль линий тока, и вектора скорости , то есть . Где dl - скалярный параметр.

Запишем дифференциальные уравнения линий тока  в проекциях:

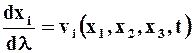 (i = 1,2,3).                                                   

Здесь - величина t - параметр.

Уравнения, описывающие закон движения или траектории движения частиц сплошной среды будут выглядеть таким образом, где t - переменная величина:

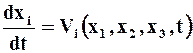  (i = 1,2,3).

То есть, линии тока не совпадают с траекториями. Совпадать они могут только в двух случаях:

1.     При установившихся движениях (тогда между двумя последними уравнениями нет различия);

2.     При неустановившихся течениях (когда поле скоростей меняется по величине, но не меняется по направлению).

Если какая-либо скалярная величина задана как функция переменных Эйлера, то в каждый момент времени можно рассматривать поверхность, где

f (x1 , x2 , x3 ,t) = const,         

которая называется поверхностью равного уровня или эквипотенциальной.

Вектор-градиент скалярной функции r в точке М – это вектор, направленный по нормали  в какой-либо точке М поверхности (1.9) в сторону роста r и равный по величине .

Вектор-градиент обозначается как grad r и вычисляется по формуле:

,

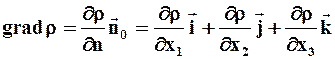где  - единичные векторы по направлению  и вдоль координатных осей.

Проекция вектора grad r на некоторое направление определяет изменение плотностей в этом направлении:

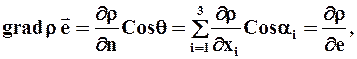
где q - угол между направлениями  и  ; Cos aI – направляющие косинусы вектора  .

Наибольшее изменение плотности происходит в направлении, нормальном к поверхности (1.9).

Поток скорости через поверхность. Если в поле скорости V (или любой другой векторной величины) мысленно провести некоторую поверхность S и в каждой точке её задать нормаль , то для определения объёма жидкости, протекающей за единицу времени сквозь поверхность S, необходимо вычислить интеграл

.

Поток скорости сквозь замкнутую поверхность S, отнесённый к единице объёма V, заключённого внутри S, называется РАСХОЖДЕНИЕМ или ДИВЕРГЕНЦИЕЙ скорости, т.е.

.

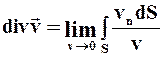В декартовой системе координат дивергенция скорости вычисляется по формуле:

.

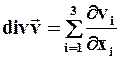Отсюда видно, что дивергенция скорости определяет скорость объёмного расширения жидкости в бесконечно малой окрестности данной точки. Поэтому поток скорости через замкнутую поверхность S должен быть равен расширению всего объёма  V жидкости внутри S, то есть

Это равенство называется формулой Гаусса.

Если в поле   мысленно проведён какой-либо замкнутый контур L, ограничивающий некоторую поверхность S, то линейный интеграл

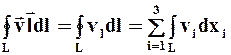
называется ЦИРКУЛЯЦИЕЙ СКОРОСТИ, а вектор, определяемый в виде

,

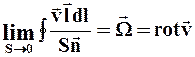называется ВИХРЕМ или РОТОРОМ скорости.

В данном случае  - единичные векторы, направленные соответственно по касательной к L  и по нормали к поверхности S.

В декартовой системе координат вихрь скорости вычисляется по формуле

.

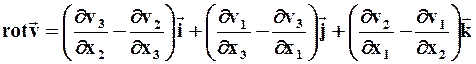На основании теоремы Стокса имеет место равенство

.

В том случае, когда все проекции скорости  могут быть определены одной функцией j(х1, х2, х3, t) в виде 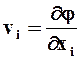 , то есть  = grad j , то говорят, что поле скоростей потенциальное, а функция   j - потенциал скорости.

 Проекция скорости vl  на любое  направление l определяется производной dj/dl .

Необходимым и достаточным условием существования потенциальных течений являются равенства (rot  = 0):

.

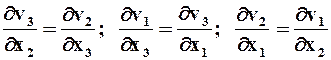Следовательно, безвихревое течение потенциально.