Определение коэффициентов  и  при истечении жидкости через малое и большое отверстие в тонкой стенке.

Рассмотрим большой резервуар с жидкостью под давлением Р0, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н0 от свободной поверхности (рис.). Жидкость вытекает в воздушное пространство с давлением Р1. Пусть отверстие имеет форму, показанную на рис., а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на (б), т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (а) Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе. Степень сжатия оценивается коэффициентом сжатия где  и  – площади поперечного сечения струи и отверстия соответственно;  и  – диаметры струи и отверстия соответственно. Запишем уравнение Бернулли для 0-0 и 1-1:  где  коэффициент сопротивления отверстия. Вводя расчётный напор  получаем , отсюда скорость истечения , где  - напор жидкости,  - коэффициент скорости   – коэффициент Кориолиса. В случае идеальной жидкости ,  следовательно, и скорость истечения идеальной жидкости  . Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения: . Произведение  и  принято обозначать буквой  и называть коэффициентом расхода, т.е. В итоге получаем расход где  – расчетная разность давлений, под действием которой происходит истечение. При помощи этого выражения решается основная задача - определяется расход. Оно применимо для всех случаев истечения. Трудность использования заключается в достаточно точной оценке коэффициента расхода  . Величина  не является расходом при истечении идеальной жидкости, так как сжатие струи будет иметь место и при отсутствии гидравлических потерь.

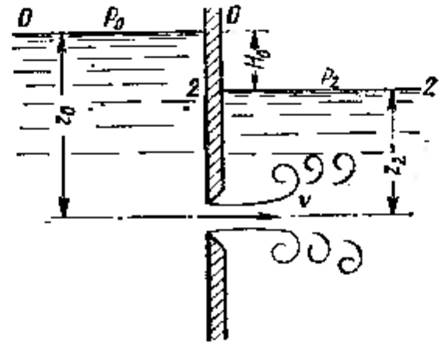
Истечение под уровень (истечение через затопленное отверстие) – истечение жидкости в закрытых руслах не в газовую среду, а в пространство, заполненное этой жидкостью. В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении. Для определения расхода  составим уравнение Бернулли для 0-0 и 2-2 (скорости считаем равными нулю ):  или  где  – расчётный напор;  – коэффициент сопротивления отверстия, имеющий примерно то же значение, что и при истечении в атмосферу;  – скорость истечения в сжатом сечении струи. Отсюда    Таким образом, имеем те же расчётные формулы, что и при истечении в воздух (газ), только расчётный напор  в данном случае представляет собой разность гидростатических напоров по обе стороны стенки, т. е. скорость и расход не зависят от высоты расположения отверстия. Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.  -  коэффициент сжатия (с - сечение струи, o - отверстия), - коэффициент расхода.