Поршень диаметром ![]() движется равномерно вниз в цилиндре, подавая жидкость Ж
в открытый резервуар с постоянным уровнем. Диаметр трубопровода
движется равномерно вниз в цилиндре, подавая жидкость Ж
в открытый резервуар с постоянным уровнем. Диаметр трубопровода ![]() , его длина
, его длина ![]() . Когда поршень находится ниже уровня жидкости в резервуаре на
. Когда поршень находится ниже уровня жидкости в резервуаре на ![]() , потребная для его перемещения сила равна
, потребная для его перемещения сила равна ![]() . Определить скорость поршня и расход жидкости в трубопроводе. Построить напорную и пьезометрическую линии для трубопровода. Коэффициент гидравлического трения трубы принять
. Определить скорость поршня и расход жидкости в трубопроводе. Построить напорную и пьезометрическую линии для трубопровода. Коэффициент гидравлического трения трубы принять ![]() . Коэффициент сопротивления входа в трубу
. Коэффициент сопротивления входа в трубу ![]() , Коэффициент сопротивления выхода в резервуар
, Коэффициент сопротивления выхода в резервуар ![]() .
.
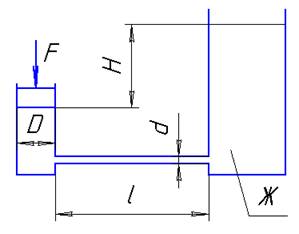
Исходные данные:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
жидкость – бензин с плотностью ![]() ;
;
Решение:
Скорость движения поршня ![]() определим по формуле:
определим по формуле:
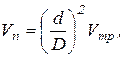 (9.1)
(9.1)
где ![]() – скорость жидкости в трубопроводе
– скорость жидкости в трубопроводе ![]() .
.
Расход жидкости ![]() в трубопроводе определим по формуле:
в трубопроводе определим по формуле:
![]() , (9.2)
, (9.2)
где ![]() – сечение трубопровода равное:
– сечение трубопровода равное:
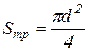 . (9.3)
. (9.3)
Скорость жидкости ![]() в трубопроводе определим исходя из величины потери напора в трубопроводе. Общую потерю напора
в трубопроводе определим исходя из величины потери напора в трубопроводе. Общую потерю напора ![]() определим по формуле:
определим по формуле:
![]() , (9.4)
, (9.4)
где ![]() – напор в цилиндре.
– напор в цилиндре.
Напор ![]() в цилиндре определим по формуле:
в цилиндре определим по формуле:
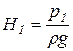 , (9.5)
, (9.5)
где ![]() – давление в цилиндре;
– давление в цилиндре;
![]() – ускорение свободного падения.
– ускорение свободного падения.
Давление ![]() в цилиндре определим по формуле:
в цилиндре определим по формуле:
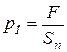 , (9.6)
, (9.6)
где ![]() – площадь поршня равная
– площадь поршня равная
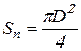 . (9.7)
. (9.7)
Формула потери напора в трубопроводе имеет вид:
![]() , (9.8)
, (9.8)
где ![]() – потеря напора при входе в трубопровод;
– потеря напора при входе в трубопровод;
![]() – потеря напора при выходе из трубопровода;
– потеря напора при выходе из трубопровода;
![]() – потеря напора в трубопроводе в результате трения.
– потеря напора в трубопроводе в результате трения.
Потеря напора ![]() при входе в трубопровод определяется по формуле:
при входе в трубопровод определяется по формуле:
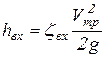 . (9.9)
. (9.9)
Потеря напора ![]() при выходе из трубопровода определяется по формуле:
при выходе из трубопровода определяется по формуле:
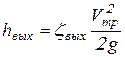 . (9.10)
. (9.10)
Потеря напора ![]() в трубопроводе в результате трения определяется по формуле:
в трубопроводе в результате трения определяется по формуле:
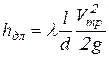 . (9.11)
. (9.11)
Подставив выражения (9.9), (9.10) и (9.11) в формулу (9.8) получим:
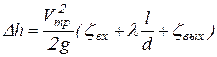 , (9.12)
, (9.12)
Из формулы (9.12) выражаем ![]() и получаем:
и получаем:
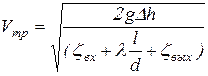 , (9.13)
, (9.13)
Подставив выражение (9.7) в (9.6) получим давление ![]() в цилиндре:
в цилиндре:
![]() , (9.14)
, (9.14)
Подставив выражение (9.14) в (9.5), а полученное выражение в (9.4) получим общую потерю напора ![]() :
:
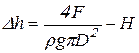 , (9.15)
, (9.15)
Подставив выражение (9.15) в (9.13) получим скорость жидкости ![]() в трубопроводе:
в трубопроводе:
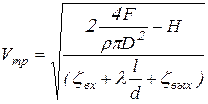 , (9.16)
, (9.16)
Полученное выражение (9.16) подставляем в (9.1) получая скорость поршня ![]() :
:
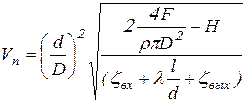
Также выражение (9.16) и (9.3) подставляем в (9.2) и получаем расход жидкости ![]() :
:
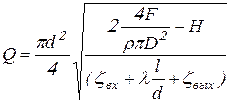
Вычисляем значения ![]() и
и ![]() :
:
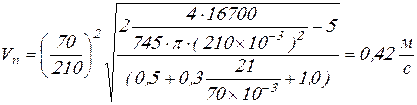 ;
;
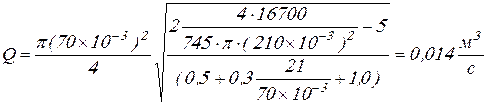 .
.
Построим напорную и пьезометрическую линии трубопровода.
Прежде всего, построим напорную линию. Для этого определим величину напора ![]() в цилиндре:
в цилиндре:
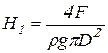 .
.
В сечении ![]() отложим от уровня жидкости
отложим от уровня жидкости ![]() по вертикали вниз отрезок
по вертикали вниз отрезок ![]() , равный потере напора при входе в трубу:
, равный потере напора при входе в трубу:
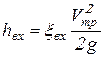 .
.
На участке трубы между сечениями ![]() и
и ![]() имеет место потеря напора на трение по длине.
имеет место потеря напора на трение по длине.
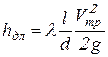 .
.
Тогда для получения точки, принадлежащей напорной линии в конце данного участка, т.е. в сечении ![]() необходимо из полного напора в сечении
необходимо из полного напора в сечении ![]() вычесть указанную потерю напора на единицу длины, и поэтому напорная линия изобразится наклонной прямой
вычесть указанную потерю напора на единицу длины, и поэтому напорная линия изобразится наклонной прямой ![]() .
.
В сечении ![]() из-за внезапного расширения трубы при выходе в резервуар происходит местная потеря напора
из-за внезапного расширения трубы при выходе в резервуар происходит местная потеря напора ![]() , поэтому откладываем вниз по вертикали отрезок
, поэтому откладываем вниз по вертикали отрезок ![]() равный:
равный:
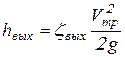 .
.
Для построения пьезометрической линии необходимо из ординат напорной линии вычесть отрезки, соответствующие значениям скоростных напоров, которые могут быть определены по уравнению Бернулли и уравнению постоянства расхода. В данном случае пьезометрическая линия представляет собой ломаную линию ![]() .
.
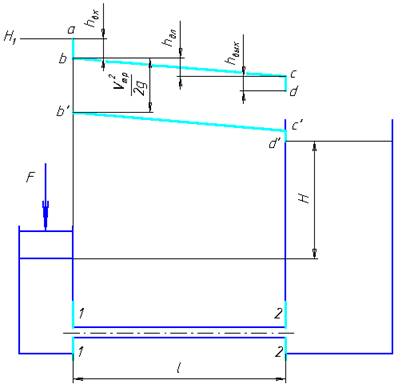
рис. 1. Напорная и пьезометрическая линии
Ответ: скорость поршня ![]() , расход жидкости
, расход жидкости 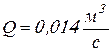 .
.
Поможем написать любую работу на аналогичную тему

