Задача №4 - Задачи по дисциплине Гидравлика

Определить время закрытия задвижки, установленной на свободном конце стального водопровода диаметром , длиной  с толщиной стенки , при условии, чтобы максимальное повышение давления в водопроводе было в три раза меньше, чем при мгновенном закрытии задвижки. Через сколько времени после мгновенного закрытия задвижки повышение давления распространиться до сечения, находящегося на расстоянии  от задвижки?

Исходные данные:

; ; .

Решение:

По условию задачи имеет место равенство:

                                                                                                       (21.1)

где  – повышение давления при мгновенном закрытии задвижки;

 – повышение давления при закрытии задвижки за время .

Время  распространения давления на расстояние  после мгновенного закрытия задвижки определим по формуле:

                                                         ,                                            (21.2)

где  – скорость распространения волны давления.

Повышение давления  при мгновенном закрытии задвижки определяется по формуле:

                                                        ,                                           (21.3)

где  – плотность жидкости;

 – скорость движения жидкости.

Повышение давления  при закрытии задвижки за время  определяется по формуле:

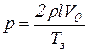                                                         ,                                            (21.4)

где  – длина трубопровода.

Скорость распространения волны давления  определяется по формуле:

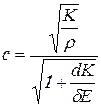                                                        ,                                          (21.5)

где  – модуль упругости жидкости;

 – модуль упругости материала стенок трубопровода.

Подставляем выражение (21.5) в (21.3) получаем формулу повышения давления  при мгновенном закрытии задвижки:

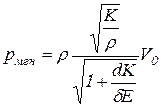                                                  .                                    (21.6)

Выражения (21.4) и (21.6) подставляем в равенство (21.1), сокращаем скорости  и плотности , далее выражаем  и результате получаем время закрытия задвижки:

                                                  .

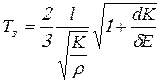Подставим выражение (21.5) в (21.2) и получим формулу времени распространения давления :

                                                  .

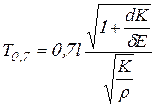Вычисляем время закрытия задвижки :

                               .

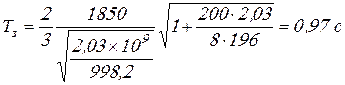Вычисляем время распространения давления :

                                  .

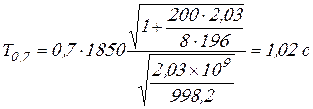Ответ: Время закрытия задвижки , время распространения волны давления .