При изучении движения реальных жидкостей встречается много трудностей потому, что на характер движения влияют многие факторы. Первым этапом изучения процесса является отбор определяющих этот процесс факторов, то есть выявление факторов, влияющих на изучаемый процесс, и исключение из рассмотрения тех из них, которые оказывают пренебрежимо малое влияние.
Следующий этап изучения – это установление зависимости интересующей величины от системы выбранных определяющих параметров. Этот этап может решаться двумя путями: аналитическим, основанным на законах физики, и экспериментальным. Первый путь применим лишь для ограниченного числа задач и при том обычно лишь для упрощенных моделей явлений. Экспериментальный путь изучения в принципе может учесть многие факторы, но он требует научно обоснованной постановки опытов, планирования эксперимента, ограничение его объема необходимым минимумом и систематизации результатов опытов. При этом часто опыты проводятся не с реальными явлениями, а с их моделями, так как параметры реальных явлений часто бывают неудобными для их изучения в лаборатории. Например, неудобно изучать в лабораторных условиях течение нефти в магистральном нефтепроводе из-за его большого диаметра, больших и очень мощных насосных установок, пожароопасности жидкости и т.п. Таким образом, необходимо принять обоснованные параметры модели. Эти задачи позволяет решить теория гидродинамического подобия. Гидродинамическое подобие складывается из трех составляющих: геометрического, кинематического и динамического подобия.
Геометрическое подобие, как известно из геометрии, предполагает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимается подобие тех поверхностей, которые ограничивают потоки, то есть подобие русел или каналов. При этом подобными должны быть не только русла в пределах изучаемого участка, но и непосредственно перед и за ними, так как они будут оказывать влияние на характер течения жидкости на изучаемом участке. Отношение двух сходственных размеров подобных русел назовем линейным масштабом и обозначим через kL. Эта величина одинакова (idem) для подобных русел I и II:
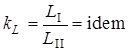 .
.
Кинематическое подобие означает пропорциональность местных скоростей в сходственных точках и равенство углов, характеризующих направление этих скоростей:
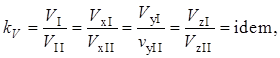
где kV – масштаб скоростей, одинаковый при кинематическом подобии.
Так как
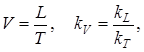
где T – время, kT – масштаб времени.
Очевидно, что для кинематического подобия необходимо геометрическое подобие русел.
Динамическое подобие – это пропорциональность сил, действующих на сходственные объемы в кинематически подобных потоках и равенство углов, характеризующих направление этих сил.
В потоках жидкости обычно действуют разные силы: силы давления, вязкости, тяжести и др. Соблюдение этих пропорциональностей означает полное гидродинамическое подобие. Осуществить полное подобие на практике удается далеко не всегда, поэтому часто имеют дело с частичным (неполным) подобием, при котором пропорциональны только лишь основные, главные силы.
Для напорных течений в закрытых руслах, то есть для потоков в трубах, в гидромашинах и т. п., такими силами являются силы давления, вязкости и инерции. На жидкость действует также сила тяжести, но в напорных потоках ее действие проявляется через давление: pпр = p + grh, то есть она учитывается.
Силы инерции определяются произведением массы на ускорение F = ma, а их отношение в подобных потоках равно масштабу сил:
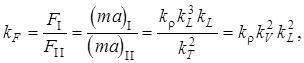
где kr – масштаб плотностей.
Таким образом, силы инерции пропорциональны плотности, квадрату скорости и размеру L во второй степени, то есть площади S:
![]()
Силы инерции примем за основу и другие силы будем сравнивать с инерционными, то есть с ![]()
Таким образом, для гидродинамического подобия потоков необходимо, чтобы
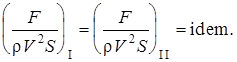
Это отношение называют числом Ньютона и обозначают Ne. Под силой F здесь понимается основная сила: сила давления, вязкости, тяжести или др. То есть это общий вид закона гидродинамического подобия.
Рассмотрим три характерных случая воздействия на движущуюся жидкость основных сил и найдем условия подобия потоков.
1. На жидкость действуют лишь силы давления и инерции. Тогда F = DpS ~ DpL2 и условие гидродинамического подобия примет вид:
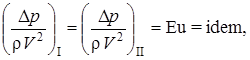
где Dp – разность давлений или просто давление,
Eu – безразмерный критерий, число Эйлера.
Таким образом, в этом случае условием гидродинамического подобия потоков является равенство чисел Эйлера, которые равны величине, пропорциональной отношению сил давления к силам инерции.
2. На жидкость действуют силы вязкости, давления и инерции. Тогда 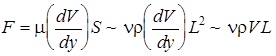 . Условие гидродинамического подобия потоков после деления на rV 2L2 примет вид:
. Условие гидродинамического подобия потоков после деления на rV 2L2 примет вид:
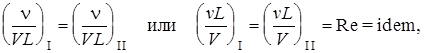
где Re – безразмерный критерий, называемый числом Рейнольдса.
Следовательно, условием гидродинамического подобия геометрически подобных потоков является равенство чисел Рейнольдса, подсчитанных для сходственных сечений потоков.
Число Рейнольдса – основной критерий подобия напорных потоков. За характерный размер L при вычислении Re принимается поперечный размер потока, например, диаметр сечения (гидравлический диаметр).
Из определения числа Рейнольдса видно, что это величина, пропорциональная отношению сил инерции к силам вязкости.
3. На жидкость действуют силы тяжести, давления и инерции. Тогда F ~ grL3 и условие гидродинамического подобия потоков примет вид:
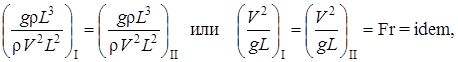
где Fr – безразмерный критерий, число Фруда.
Следовательно, условием гидродинамического подобия геометрически подобных потоков является равенство чисел Фруда. Из вывода видно, что число Фруда – это величина, пропорциональная отношению силы инерции к силе тяжести. Этот критерий важен при рассмотрении безнапорных течений в открытых руслах, для напорных течений его можно не учитывать.
Рассмотрим два гидродинамически подобных потока идеальной жидкости. Запишем уравнение Бернулли для двух сечений одного из потоков при условии, что геометрическая высота сечений постоянна:
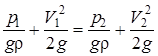
Используя уравнение расхода V1S1 = V2S2, исключим скорость V1 и, перегруппировав члены уравнения, приведем его к безразмерному виду:
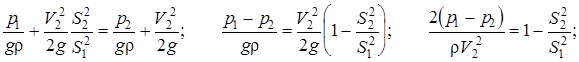
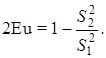
Правая часть уравнения одинакова для подобных потоков вследствие геометрического подобия, а левая – вследствие динамического подобия, и все уравнение одинаково для подобных потоков идеальной жидкости. Таким образом, для обеспечения гидродинамического подобия напорных потоков идеальной жидкости достаточно одного геометрического подобия.
Теперь запишем уравнение Бернулли для одного из напорных потоков реальной (вязкой) жидкости, подобных гидродинамически:
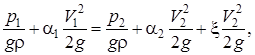
где x – коэффициент потерь энергии между рассматриваемыми сечениями.
После приведения этого уравнения к безразмерному виду получим
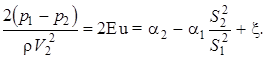
Число Эйлера одинаково для динамически подобных потоков; коэффициенты Кориолиса для сходственных сечений одинаковы из-за кинематического подобия потоков, следовательно, одинаков будет и коэффициент потерь энергии x, а также все уравнение. Если рассматриваются подобные потоки в трубах постоянного сечения, то будет одинаков и коэффициент потерь на трение по длине l, о котором мы подробно поговорим несколько позже.
Итак, в подобных напорных потоках имеем равенство безразмерных коэффициентов и чисел a, x, l, Eu, Re и некоторых других. Изменение числа Рейнольдса, означает, что изменилось соотношение основных сил в потоке, в связи с чем указанные коэффициенты тоже могут несколько измениться. Поэтому все коэффициенты следует рассматривать как функции числа Рейнольдса, хотя в некоторых интервалах числа Рейнольдса они могут оставаться постоянными.
При экспериментальных исследованиях и моделировании напорных течений в лабораторных условиях необходимо:
– обеспечить геометрическое подобие модели (I) и натуры (II), включая условия входа и выхода;
– соблюсти равенство чисел Рейнольдса: ReI = ReII.
Из второго условия можно получить необходимую скорость потока при эксперименте
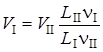 .
.
В частном случае, если nI = nII скорость при эксперименте должна быть больше натурной в L II/L I раз. Если применить менее вязкую жидкость или ту же, но при повышенной температуре, можно снизить скорость VI.
Кроме перечисленных основных критериев подобия (Eu, Re, Fr), в гидравлике применяют и другие критерии для особых случаев течения жидкости.
При рассмотрении течений, связанных с поверхностным натяжением (при распылении струи на капли), вводят критерий Вебера (We), пропорциональный отношению сил поверхностного натяжения к силам инерции:
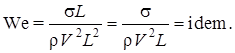
При рассмотрении нестационарных периодических течений с периодом T (например, течение в трубопроводе, подсоединенном к поршневому насосу) вводят критерий Струхаля (Sh), учитывающий силы инерции от нестационарности, которые пропорциональны массе (rL3) и ускорению (дV/дt), то есть V/T. Следовательно, условием гидродинамического подобия в этой ситуации будет
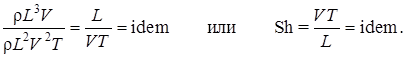
При рассмотрении движения жидкости с учетом ее сжимаемости (например, движений эмульсий) вводят критерий Маха (М), учитывающий силы упругости, которые пропорциональны площади (L2) и объемному модулю упругости K = r c2. Поэтому силы упругости пропорциональны r c2L2. Условие гидродинамического подобия при этом
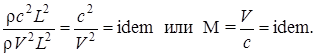
Критерий Маха очень важен при рассмотрении движения газа. Чем ближе M к 1, тем больше влияние сжимаемости газа на его движение. В применении к жидкостям вместо числа Маха иногда используют число Коши, равное
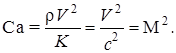
Поможем написать любую работу на аналогичную тему

