Кинематика жидкости отличается от кинематики твердого тела, у которого все точки жестко соединены между собой. В жидкости частицы могут перемещаться относительно друг друга. Задачей кинематики жидкости является определение скорости в любой ее точке, то есть определение поля скоростей.
В гидравлике существуют понятия идеальной и реальной жидкости. Идеальной жидкостью называют абстрактную модель жидкости, абсолютно лишенной вязкости и несжимаемой. Реальная жидкость всегда рассматривается как вязкая, а сжимаемостью часто пренебрегают.
Рассмотрим движение идеальной жидкости. В такой жидкости, как и в неподвижной, возможны тоже только сжимающие нормальные напряжения, то есть гидромеханическое давление. Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости: на внешней поверхности жидкости оно направлено по внутренней нормали, а в любой другой точке – по всем направлениям одинаково.
Течение жидкости может быть установившимся (стационарным) и неустановившимся (нестационарным).
Установившимся называется течение, неизменное во времени, при котором давление и скорость являются только функциями координат, но не зависят от времени. Давление и скорость могут изменяться при перемещении частицы жидкости, но в данной неподвижной относительно русла точке давление и скорость во времени не изменяются:
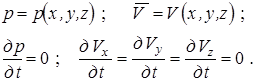
В частном случае стационарное течение жидкости может быть равномерным, когда скорость каждой частицы не изменяется при изменении ее координат, и поле скоростей остается неизменным вдоль потока.
Неустановившимся называется течение жидкости, все характеристики которого (или некоторые из них) изменяются во времени в точках рассматриваемого пространства:
![]()
Исследовать установившиеся течения значительно проще, чем неустановившиеся. В дальнейшем мы будем чаще всего вести речь об установившихся течениях. Траектории частиц при стационарном течении неизменны во времени. При нестационарном течении траектории частиц, проходящих через данную точку пространства в различные моменты времени, могут иметь различную форму. Поэтому для рассмотрения картины течения вводится понятие линии тока.
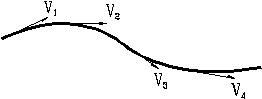
Рис. 16. Линия тока
Линия тока (Рис. 16) – это кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной.

Рис. 17. Трубка тока
Если в движущейся жидкости взять бесконечно малый замкнутый контур и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока (Рис. 17). Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.
В любой точке трубки тока скорости частиц жидкости направлены по касательной, нормальная к этой поверхности составляющая скорости отсутствует, следовательно, при установившемся движении ни одна частица жидкости ни в одной точке не может проникнуть внутрь струйки или выйти наружу. Таким образом, трубка тока является как бы непроницаемой стенкой, а элементарная струйка – это самостоятельный элементарный поток.
Живым сечением потока называется поверхность в пределах потока, проведенная нормально к линиям тока. Если элементарные струйки проходят параллельно, то живое сечение потока будет плоским.
Смоченным периметром h называют длину линии соприкосновения жидкости с твердыми стенками в данном живом сечении.
Гидравлическим радиусом называют отношение площади живого сечения потока к смоченному периметру:
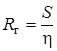 .
.
Гидравлический диаметр равен 4 гидравлическим радиусам:
Dг = 4Rг.
Легко убедиться, что для круглого сечения Rг = 0,5R, а Dг = D.
Чаще всего живое сечение имеет форму круга, но если форма сечения иная, то в формулы подставляют эквивалентный гидравлический диаметр.
Различают напорное и безнапорное течение. Напорным называют течение в закрытых руслах без свободной поверхности, а безнапорным – течение со свободной поверхностью. При напорном течении давление обычно вдоль потока переменное, при безнапорном – постоянное (на свободной поверхности) и чаще всего атмосферное. В данном курсе мы будем рассматривать напорные течения.
Поможем написать любую работу на аналогичную тему

