Методы экспертных оценок
Методы, основанные на интуиции и опыте, – эвристические методы, используют в решении наиболее сложных проблем, в особенности в условиях неопределенности, которая возникает из–за недостатка информации или неустойчивости развития.
Теория катастроф
Теория катастроф представляет собой исследовательскую программу изучения и прогнозирования неустойчивости различных систем. Такое название она получила потому, что потеря устойчивости по своим проявлениям может быть катастрофична, даже если не приводит к гибели или разрушению системы, а лишь обуславливает переход к иной траектории развития.
Простейшая программа прогнозирования элементарной катастрофы в экономической или производственной системе может быть построена на основе данных связи переменных, характеризующих ее поведение. Функции, описывающие эти связи, могут быть получены эконометрическими методами.
Например, связь двух переменных величин можно представить уравнением:
![]() , (8)
, (8)
где у и х – переменные; а – параметр; множитель 1/3 в первое слагаемое введен для упрощения преобразований.
Уравнение (8) представляет собой функцию, характер которой определяется величиной параметра а. Если этот параметр положителен, то функция носит монотонный характер, ее график – плавная монотонно возрастающая кривая. Но если параметр а уменьшается, то при нулевом его значении тип функции меняется. При нулевом значении параметра изменяется характер связи в системе и поведение системы, это изменение называют бифуркацией. При отрицательной величине параметра а функция, описываемая уравнением (8) представляет собой немонотонную функцию. Она имеет максимум и минимум при значениях х = ± а½.
Катастрофа. Связь между переменными в определенной окрестности начала координат будет не однозначной. Одному значению переменной у будут соответствовать теперь три разных по величине значения переменной х. Таким образом, при монотонном плавном изменении переменной у переменная а будет изменяться скачкообразно. Это и будет катастрофа.
Если установлено, что между переменными, характеризующими поведение системы, связь описывается уравнением вида (8), то можно утверждать, что в системе возможно проявление неустойчивости.
Если параметр а положителен, но выявлена тенденция его уменьшения, то можно считать, что система приближается к катастрофе. В обоих случаях необходимо продолжить изучение системы и выявить условия или возможные сроки наступления катастрофы, оценить ее вероятные последствия.
Тип элементарной катастрофы, определяемой связью, которая описывается уравнением (8), носит название катастрофы складки, поскольку в пространстве трех координат – двух переменных и параметра а – поверхность, описываемая уравнением, имеет вид складки, начинающейся при а = 0 и углубляющейся по мере дальнейшего уменьшения параметра. На рис. 2 показаны поверхности катастрофы складки и возможные траектории развития систем в условиях катастрофы этого типа.
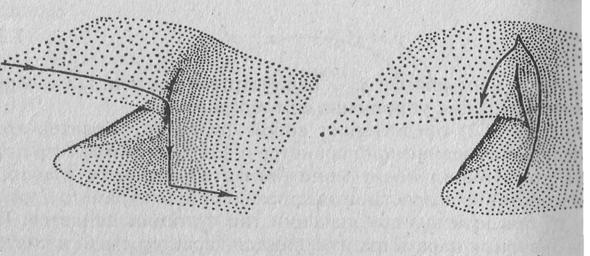
Рис. 2. Геометрия катастрофы складки и возможные траектории развития системы
Элементарная теория катастроф основывается на теореме Тома и классификации Арнольда. Они определили простейшие формы устойчивых и неустойчивых связей в системах – формы катастроф.
Возможность появления элементарных катастроф связана с оценкой возможности описания связей в системах уравнениями типа уравнений элементарных катастроф (8).
На практике это может быть реализовано, если можно получить регрессионное уравнения связей в системах. Уравнения устойчивых связей имеют вид:
F=x1 +x12 +M, (9)
F =x1 +x2+x1*x2+x22+x12+ N, (10)
где F – функция, которая может быть приравнена к еще одной переменной в первой степени или любой постоянной величине, например нулю; М – функция вида х22+…хi2 – xi+12 – … – xn2, (1≤i≤n); N – функция вида х32+…+хi2+xi+12 – xi+12 – … – xn2, (2≤i≤n); хi – взаимосвязанные переменные, характеризующие систему.
Все члены уравнения указаны с точностью до постоянных множителей.
Если по уравнению детерминации, уровню значимости регрессионное уравнение одной из катастроф превосходит регрессионное уравнение связи устойчивого характера, то следует считать катастрофу возможной и дать ее прогноз.
Флаги катастроф представляют собой косвенные признаки, по которым можно судить о возможности наличия катастрофы в системе. К сожалению, для экономических и производственных систем при эмпирическом рассмотрении можно с уверенностью указать лишь один признак, флаг. Этот флаг — аномальная дисперсия.
Признаком всевозможного приближения катастрофы является нарастание дисперсии или размахов величин, характеризующих систему. Это флаг, как известно, успешно реализуется при статистическом регулировании качества продукции в серийном и массовом производстве.
Поможем написать любую работу на аналогичную тему

