Как реальные газы при определенных температурах и давлениях по своим свойствам близки идеальным газам, так и реальные растворы при определенных условиях разбавления приближаются к идеальному раствору.
Идеальным является такой раствор, вкотором свойства, присущие растворителю и растворенному веществу, не меняются из-за присутствия новых компонентов, если не считать возможных изменений этих свойств при разбавлении.
Стремление к улетучиванию для молекул растворителя или растворенного вещества уменьшается только в той мере, в которой наличие молекул другого компонента пространственно затрудняет или вообще делает невозможным уход молекул из раствора. В случае идеальных растворов объем является аддитивным, а температура при смешивании не изменяется.
В реальных растворах растворитель и растворенное вещество взаимодействуют друг с другом. Например, если спирт обладает низкой летучестью из-за сильного диполь-дипольного взаимодействия, то при смешивании его с бензолом вследствие разделения диполей полярные молекулы спирта легче переходят в газовую фазу, и парциальное давление его пара будет выше. Возможно и наоборот в случае, например, растворения неполярного вещества в полярном растворителе.
Для того, чтобы применять законы для идеальных растворов в случае реальных, необходимо введение некоторых ограничений. Один из таких принципов носит название предельного закона. Он гласит, что если содержание растворенных молекул в растворе относительно мало, то взаимодействие между ними будет минимальным и, следовательно, они будут слабо влиять на поведение растворителя.
Таким образом, законы идеальных растворов можно применять к реальным растворам, если речь идет о разбавленных. Для рассмотрения свойств реальных растворов при относительно высоких концентрациях растворенного вещества имеются также уравнения, однако они достаточно сложны.
Прежде чем приступить к обсуждению некоторых относительно простых уравнений, тем не менее, позволяющих рассчитывать давление пара, точку замерзания, точку кипения, а также осмотическое давление растворов, познакомимся с двумя фундаментальными соотношениями, лежащими в основе предельных уравнений, – с правилом фаз и уравнением Клаузиуса-Клапейрона.
Правило фаз. На рис. 6.1 показана фазовая диаграмма, количественно описывающая поведение гетерогенной системы, содержащей гомогенные области-фазы. Фазы отделены друг от друга заметными границами, которые называют поверхностями раздела. Каждая фаза гомогенна, однако она не непрерывна. Число фаз равно числу отделенных друг от друга структур, существующих в различных физических состояниях в системе. В одной системе могут существовать несколько жидких или твердых фаз, например: вода – масло, лед – твердая соль. Различают как число фаз, так и число компонентов, образующих фазу. Под числом компонентов понимают число независимых химических индивидуальностей. На рис. 6.1 показана хорошо известная фазовая диаграмма воды. Она является однокомпонентной. Если в воде растворить соль, то получим двухкомпонентную систему. Если растворить два белка в буфере, получим пятикомпонентную систему – два белка, вода, соль и кислота.
Изучение гетерогенных систем сильно упростилось после предложенного в 1874 году Гиббсом обобщения, которое получило название «правило фаз». Оно состоит из очень простого соотношения: а = с – р + 2, где с – число компонентов системы, р – число фаз и f – число степеней свободы системы, т.е. число независимых переменных – таких, как температура, давление и концентрация, которые необходимы для полного описания системы.
Согласно альтернативной формулировке правила фаз, число степеней свободы – это число независимых переменных, которые могут быть изменены без изменения числа фаз. Правило фаз применимо только для систем, находящихся в равновесии.
Посмотрим на фазовую диаграмму воды. Поскольку вода является единственным компонентом, значит с = 1. Вода существует в трех фазах – твердой, жидкой и газообразной. При этом число фаз, которые существуют в равновесии, зависит от температуры и давления.
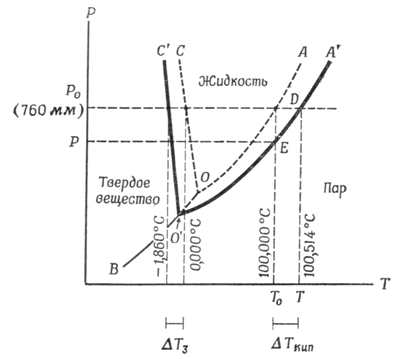
Рис. 6.1. Фазовая диаграмма воды и гипотетического 1 т идеального раствора (масштаб не соблюдается)
Линия ОА представляет собой кривую давления паров воды. Вдоль этой линии вода и пар находятся в равновесии друг с другом. Экспериментально такую линию получают путем измерения давления пара чистой воды при разных температурах.
Линия ОВ является кривой сублимации льда. Выше этой кривой вода существует в виде льда, ниже – в виде пара. В равновесии лед и пар находятся только вдоль линии ОВ, которая и является границей этих двух фаз.
Линия ОС описывает зависимость точки плавления льда от давления; лед и жидкая вода этой линии находятся в равновесии. Наклон линии ОС относительно оси ординат указывает на то, что при увеличении давления точка плавления льда понижается. Три кривые имеют общую точку пересечения 0, известную под названием «тройной точки».
Поможем написать любую работу на аналогичную тему

